定義
塞曼效應中的朗德g因子由下式給出
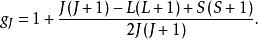朗德因子式中L,S,J分別是原子能態（光譜支項）的角量子數、自旋量子數和內量子數。
推導
朗德假定，當兩個角動量 Lħ與 Sħ耦合時，它們的相互作用能由下式給出：
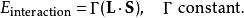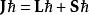朗德因子
朗德因子令，為耦合後的總角動量，則可以證明，在上述形式的相互作用能下， Lħ與 Sħ將繞矢量 Jħ進動。
在外加磁場的作用下，帶電粒子的角動量會繞外加磁場的方向進動。在這種情況下，是 Jħ進行進動。朗德採用了一種簡化處理的方法，即認為外磁場中的原子的能量僅僅與矢量 Lħ與 Sħ的長時間平均值有關，而後者恰好就是它們在 Jħ方向上的投影，即
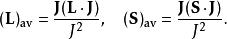朗德因子隨後，朗德進一步假定，角動量 Lħ貢獻的磁能由經典的公式給出，並假定 Jħ是量子化的，其沿著磁場方向的分量由磁量子數M確定，即
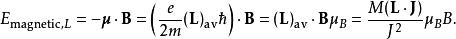朗德因子式中 μ是磁矩，而 μ為玻爾磁子。類似地，朗德寫出了角動量 Sħ帶來的能量貢獻，但他發現為了與實驗結果相一致，需要加上額外的因子 2。當時朗德並不清楚為什麼，現在我們知道這就是電子的自旋g因子。即：
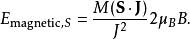朗德因子將上面結果加起來，朗德得到下列的表達式，並引入符號g，這就是朗德g因子的最早來源：
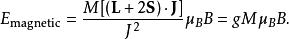朗德因子利用關係式 L+ 2S= J+ S，朗德得到：
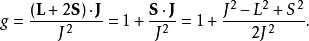朗德因子但是，朗德發現，為了與實驗結果相符，這一表達式需要修改為下式，當時朗德並不清楚原因。現在來看，只要將上面的角動量矢量都作為算符來處理，然後將對應的角動量平方算符用其本徵值取代，得出這個結果是很自然的。
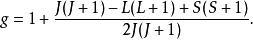朗德因子推廣
從上面的導引可見，定義朗德g因子的式子是
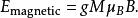朗德因子上式可以等價地表述為：
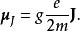朗德因子很自然的推廣是將兩邊的J同時換成L、S等，並對不同的粒子將m換成對應粒子的質量。這就是現在廣泛使用的朗德g因子。
粒子物理學
粒子物理學中的g因子是自旋g因子，根據自旋角動量和自旋磁矩按照上面的形式定義。
電子
上面的導引已經給出了電子自旋g因子的定義。在實際使用中，它的符號有兩種取法，用不同的符號表記：
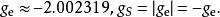朗德因子歷史上，它的理論值有過變動：
（1）在非相對論量子力學理論下考慮自旋-軌道作用時，等效地說，g為1。
（2）若再額外考慮狹義相對論時間展長效應下的湯瑪斯進動修正（1927年），g變為2，方合乎當代實驗觀測值。
（3）在相對論量子力學，也就是指保羅·狄拉克所提出的理論（1928年），g恰恰為2；並不如前者采外加修正的方法，是具有一致性的理論可導出的自然結果。
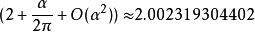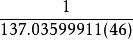朗德因子
朗德因子（4）在量子電動力學（QED）中，因為電子與真空能量的電磁漲落相互作用，可表為單環費因曼圖，提出QED的朱利安·施溫格等人（1947年）所得的g理論值為；α目前被視為是自然常數之一，其值約為。
（5）威利斯·蘭姆等人實驗觀測到的蘭姆位移效應，所得g觀測值為 2.002 319 304 376 8（86），與理論相符精準度達小數點下第9位，展現出量子電動力學等現代物理理論所能達到的驚人精準預測程度。
其它粒子
一些粒子的朗德g因子列表如下：
| 粒子 | 朗德g因子 | Δg |
| 電子 | -2.002 319 304 361 53 | 0.000 000 000 000 53 |
| 中子 | -3.826 085 45 | 0.000 000 90 |
| 質子 | 5.585 694 713 | 0.000 000 046 |
| 渺子 | -2.002 331 8418 | 0.000 000 0013 |
