有限跡

設tr(·)是퓜+上的跡，若對一切A∈퓜，有tr(A)

簡介

跡

跡是矩陣跡概念的推廣。設 是馮·諾伊曼代數，為屬於 的正運算元全體，如果tr(A) 是上的非負實值（不恆為0，可以取值+∞）泛函，滿足：

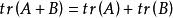有限跡

1、 ;

2、當λ≥0時，tr(λA)=λtr(A)；

3、對於 內任意酋運算元 V，有

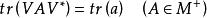有限跡

則稱 tr(·)是上的跡。

定義

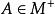有限跡

若對一切 ，有tr(A)<+∞，則稱tr為有限跡。

推廣

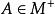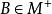有限跡

有限跡

若對使得tr(A)=+∞的任一 ，必有 ，使得 A≥B≠0，而且tr(B)<+∞，則稱tr(·)是半有限跡。

若當{A}為的向上有向族，且 A 為此族的上確界時，總有tr(A)=sup tr(A)，則稱 tr 為正規跡。

馮·諾伊曼代數

亦稱弱閉對稱運算元環，是一類由運算元構成的弱閉的C*代數。

令(H)為希爾伯特空間H上有界線性運算元全體所成的C*代數，其中∗運算為取共軛。如果是(H)的含恆等運算元I的巴拿赫∗子代數（即自伴子代數），且關於(H)的弱運算元拓撲是閉的，則稱為馮·諾伊曼代數，常簡稱v.N.代數（關於運算元範數拓撲為閉的巴拿赫∗子代數是C*代數）。