有限質點法

簡介

有限質點法是一種新穎的結構分析方法，它以向量力學和數值計算為基礎，將結構離散為質點群，並採用牛頓第二定律描述這些質點的運動，避免求解非線性方程組和整體剛度矩陣，特別適合於計算發生剛體位移和幾何大變形的結構或機構。

有限質點法是向量力學與數值計算相結合的一種結構分析方法。向量力學是Ting教授提出的一種物理力學模式，不同於傳統力學以函式和數學體來描述結構，向量力學以離散的質點來描述結構，結構的質量均集中在質點上。每個質點的運動遵循牛頓第二定律。

有限質點法

各質點間通過單元連線。單元沒有質量，因此在外力作用下處於靜平衡狀態。可以由單元的質量平均分配到節點得到；的計算將在下文中給出。質點的外力可以是質點受到的集中力，也可以是作用在結構單元上的均布外力轉化來的等效外力。等效外力的求解方法與有限元方法相同。整個結構任意時刻的各個質點在內力和外力的共同作用下處於動平衡狀態。質點的加速度可由顯示積分法表示為位移和時間的表達式。因此，整個結構實際上是在每一個時間步對每一個質點求解控制方程式，以得到結構各質點在各時間步的位移，進而求得整個結構的運動行為。

基本理論

以有限個離散的質點的空間坐標來描述結構，質點的性質來描述結構的性質，質點的性質包括坐標、質量(也包括質量慣性矩)、作用力、廣義運動和運動約束，用以表示結構的空間位置、幾何形狀、質量、受力、變形和邊界條件。

有限質點法

有限質點法

以質點軌跡模擬結構的運動，用有限個質點在微小時間段上的運動去逼近結構在空間和時間上的連續運動。圖2為採用兩個質點描述的構件運動，構件在fD時刻的位置為AB，在t時刻運動到位置CD。將構件由AB到CD的運動路徑以單位時間△t為間隔，劃分為有限個微小的運動，如質點由A到C經歷了 。質點在△t時問段上的運動稱為路徑單元。在途經單元內質點的性質(如內力、質量、數量、和拓撲關係)在路徑單元內不發生改變，並以途經單元開始時刻的結構構形作為參考構形。各質點的運動遵循牛頓第二定律，如下式：

有限質點法

(1)

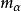有限質點法

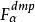有限質點法

有限質點法

有限質點法

有限質點法

有限質點法

有限質點法

式中， 為質點口的質量； 以為質點α的加速度： 和 分別為質點α的內力向量和外力向量。 為阻尼力， ，μ為阻尼係數， 為質點α的加速度。

求解式(1)的方法很多。有限質點法採用顯式時間積分法求解，主要是為了避免使用隱式解法帶來複雜的疊代和收斂問題。顯式時間積分法的優點是公式清晰簡單，不需使用程式疊代。採用中央差分公式描述質點的加速度，可得已知外力情況下的位移公式：

有限質點法

(2)

如果己知結構的運動路徑，求解結構的外力情況，則可以選用位移控制法，由式(2)按下式求解：

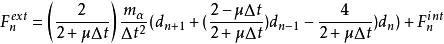有限質點法