基本內容
對於一個運輸問題，如果存在非唯一最優解，就稱該運輸問題存在多重最優解。
對於一個存在多重最優解的運輸問題，求得第一個最優解之後，在後續的最優解求解過程中，若基變換的調整量等於最小運量或者零，那么這樣得到的最優解可稱之為狹義多重最優解。
對於一個存在多重最優解的運輸問題，在求得第一個最優解之後，在後續的最優解求解過程中，若基變換的調整量可以取得從零到最小運量之間的任意一個實數，那么這樣得到的最優解就稱之為廣義多重最優解。
比較
按照多重最優解的個數是有限或無限，可以分為有限多重最優解和無限多重最優解。
對於一個存在多重最優解運輸問題，如果多重最優解的個數是有限多個，就稱該運輸問題存在有限多重最優解。
對於一個存在多重最優解運輸問題，如果多重最優解的個數是無限多個，就稱該運輸問題存在無限多重最優解。
判定定理
有限多廣義多重最優解
對於一個運輸問題，在得到的第一個最優解的最終表中，若至少存在一個檢驗數為零的非基變數，並且在以這個非基變數為出發點的閉迴路上，在需要減少運輸量的頂點中，最小的運量不等於零，那么該運輸問題存在多重最優解。若調整量只可取大於等於零的整數，那么這個運輸問題存在有限多個廣義多重最優解。
有限多狹義多重最優解
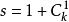有限多重最優解
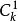有限多重最優解有限多狹義多重最優解個數下限的計算公式如下：假設存在k(k≥1)個檢驗數為零的非基變數滿足運輸問題存在多重最優解的要求，那么該運輸問題至少存在個最優解。(其中s為最佳調運方案的最少個數，為從k個非基變數中任意取一個作為入基變數的組合數。)
意義
在現實的決策過程中，決策者要考慮的因素龐雜而且帶有很大程度的不確定性，所以為其提供最為全面的決策支持信息至關重要。因此從運輸問題多重最優解出發，對其進行了進一步的細分研究，給出了分類及相關的判定定理，會充實對最優解的解系，即獲得有限多重最優解和無限多重最優解的條件及判定的研究，這對解決實際問題有重要的現實意義。
教學套用
在運輸問題的教學中，不僅應該讓學生掌握求得運輸問題最優解的方法，還應該啟發學生對問題有更深入的理解，從運輸問題多重最優解出發，獲得有限多重最優解和無限多重最優解的條件及判定的研究，抓住事物的本質，而不是停留在表面，這對培養學生抽象思維、綜合歸納能力是大有裨益的。
