緒論
通常,在經典力學裡,一維的有限位勢壘問題會設定一個粒子,從位勢壘的左邊,往位勢壘移動。假若,粒子的能量大於位勢壘的位勢。則這粒子,在經過位勢壘的時候,因為動能的轉換為勢能,速度會降低,但方向不會改變。當移動至位勢壘外時,速度又會回復至原本值。假若,粒子的能量小於位勢壘的位勢,則在與位勢壘彈性碰撞之後,這粒子會改變方向,以同樣的速率,往回移動。粒子絕對無法存在於位勢壘內或越過位勢壘。
在量子力學裡,粒子的量子行為,是取決於其波函式。由於粒子沒有被有限位勢壘束縛,粒子的能量不是離散能量譜的特殊容許值,而是大於 0 的任意值,因此不需要求算粒子的能量。在這裡,主要研究的是粒子的一維散射。這是一個很有意思的領域。假若,粒子的能量大於位勢壘的位勢。由於往位勢壘傳播的波函式,並不是完全地透射過位勢壘,仍舊有一部分反射回來。所以,反射的機率幅大於 0 ,粒子被反射回來的機率大於 0 。假若,粒子的能量小於位勢壘的位勢,雖然波函式會呈指數地遞減,在位勢壘內,機率幅仍舊大於 0 。所以,這粒子存在於位勢壘內的機率大於 0。不止這樣,機率幅在位勢壘外的另一邊也大於 0 。假若,位勢壘的位勢並不大大的超過粒子的能量,位勢壘的壘寬也並不很寬,則粒子穿越位勢壘的機率會是很顯著的,稱這效應為量子隧穿效應。透射的可能性,稱為透射係數;反射的可能性,則稱為反射係數。
定義
 有限位勢壘
有限位勢壘 有限位勢壘
有限位勢壘 有限位勢壘
有限位勢壘 有限位勢壘
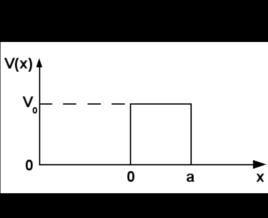
有限位勢壘一維有限位勢壘的壘寬為 ,左邊壘壁與右邊壘壁的位置分別為 x=0與 x=a 。壘外位勢為 0 。在壘壁,位勢突然升高為 。壘內位勢保持為 。這一維的位勢壘將整個一維空間分為三個區域:壘左邊,壘內,與壘右邊。在每一個區域內,對應著不同的位勢,描述粒子的量子行為的波函式也不同,標記為:
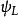 有限位勢壘
有限位勢壘:壘左邊,x<0(壘外區域),
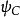 有限位勢壘
有限位勢壘:壘內,0<x<a(壘內區域),
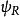 有限位勢壘
有限位勢壘:壘右邊,a<x(壘外區域)。
這些波函式,都必須滿足,一維不含時間的薛丁格方程:
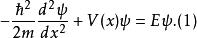 有限位勢壘
有限位勢壘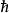 有限位勢壘
有限位勢壘其中, 是約化普朗克常數, m 是粒子質量,x是粒子位置,V(x) 是位勢,E是能量。
推導
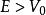 有限位勢壘
有限位勢壘在位勢壘分開的每一個區域內,位勢都是常數,粒子是半自由粒子。薛丁格方程的解答可以寫為往左與往右的波函式的疊加。假若, ,解答為
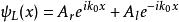 有限位勢壘
有限位勢壘, 壘左邊, x<0 (2)
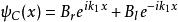 有限位勢壘
有限位勢壘, 壘內,0<x<a (3)
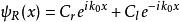 有限位勢壘
有限位勢壘, 壘右邊,a<x (4)
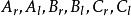 有限位勢壘
有限位勢壘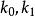 有限位勢壘
有限位勢壘其中, 都是常數,下標r與l 分別標記波函式往右或往左的方向。波數 與能量的關係,分別為
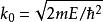 有限位勢壘
有限位勢壘, 壘左邊與壘右邊 (5)
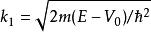 有限位勢壘
有限位勢壘, 壘內 (6)
從波函式在x=0與x=a的邊界條件,可以求得常數。波函式與其導數必須滿足連續性:
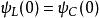 有限位勢壘
有限位勢壘,
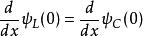 有限位勢壘
有限位勢壘,
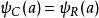 有限位勢壘
有限位勢壘,
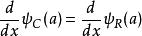 有限位勢壘
有限位勢壘。
將波函式的方程 (2) 、(3) 、(4) , 代入邊界條件的四個方程,則可得到
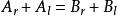 有限位勢壘
有限位勢壘,(7)
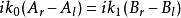 有限位勢壘
有限位勢壘,(8)
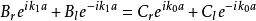 有限位勢壘
有限位勢壘,(9)
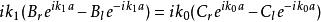 有限位勢壘
有限位勢壘。(10)
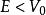 有限位勢壘
有限位勢壘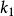 有限位勢壘
有限位勢壘假若,粒子的能量小於位勢, ,則 成為虛數,在壘內,波函式呈指數遞減。
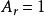 有限位勢壘
有限位勢壘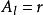 有限位勢壘
有限位勢壘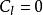 有限位勢壘
有限位勢壘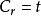 有限位勢壘
有限位勢壘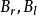 有限位勢壘
有限位勢壘設定 (粒子從左邊往位勢壘移動的波函式的波幅度), (反射幅度), (沒有粒子從右邊往位勢壘移動), (透射幅度)。將這些變數的值代入方程 (7) 、(8) 、(9) 、(10) ,則可得到常數 的關係方程:
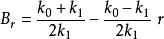 有限位勢壘
有限位勢壘,(11)
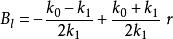 有限位勢壘
有限位勢壘,(12)
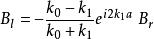 有限位勢壘
有限位勢壘。(13)
將方程 (11) , (12) 代入方程 (13) ,可求得反射幅度r:
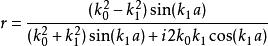 有限位勢壘
有限位勢壘。(14)
將方程 (11) , (12) , (14) 代入方程 (9) ,可求得透射幅度t:
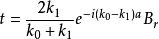 有限位勢壘
有限位勢壘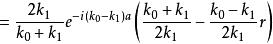 有限位勢壘
有限位勢壘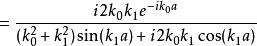 有限位勢壘
有限位勢壘因為模型的對稱性,假若計算粒子從右邊往位勢壘移動的反射幅度r和透射幅度t,答案也會相同。
套用
一維有限位勢壘問題,是一個簡單與抽象的理論問題。但是,它仍舊可以用來模擬許多實際的系統。例如,電導體的表面,時常會覆蓋著一層薄薄的氧化物。在電導體的內部,傳導電子可以自由的移動。可是,在兩個電導體的界面之間,由於這一層氧化物的阻礙,使得傳導電子的運動受到很大的影響。有限位勢壘問題可以用來模擬傳導電子從一個電導體穿越到另一個電導體的狀況,因而更加了解電流經過兩個電導體的物理內涵。
掃描隧道顯微鏡(STM) 運作的物理原理是量子隧穿效應。在這裡,位勢壘是由 STM 的尖端與檢驗物體之間的間隔造成的。由於量子隧穿效應呈指數跟位勢壘壘寬有關,這儀器可以非常靈敏地感應到,檢驗物體表面的高低不平的變化。
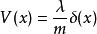 有限位勢壘
有限位勢壘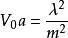 有限位勢壘
有限位勢壘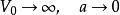 有限位勢壘
有限位勢壘Delta 位勢壘是另外一種很重要的位勢壘,可以視為一種特別的有限位勢壘。壘內位勢為狄拉克 Delta 函式,壘外位勢為 0 的位勢壘。所有在此條目導引出來的結果,都能夠套用於 Delta 位勢壘,只需要保持不變,而同時取極限。
參閱術語
•自由粒子
•無限深方形阱
•有限深方形阱
•球對稱位勢
•Delta 位勢阱
•Delta 位勢壘