定義
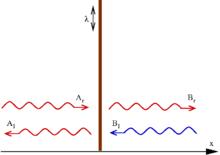 圖1.對於一個Delta位勢壘的散射
圖1.對於一個Delta位勢壘的散射一個粒子獨立於時間的薛丁格方程為
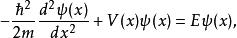 Delta位勢壘
Delta位勢壘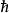 Delta位勢壘
Delta位勢壘 Delta位勢壘
Delta位勢壘 Delta位勢壘
Delta位勢壘 Delta位勢壘
Delta位勢壘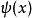 Delta位勢壘
Delta位勢壘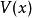 Delta位勢壘
Delta位勢壘其中, 是約化普朗克常數, 是粒子質量, 是粒子位置, 是能量, 是波函式, 是位勢,表達為
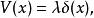 Delta位勢壘
Delta位勢壘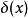 Delta位勢壘
Delta位勢壘 Delta位勢壘
Delta位勢壘其中, 是狄拉克Delta函式, 是狄拉克Delta函式的強度。
導引
 Delta位勢壘
Delta位勢壘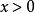 Delta位勢壘
Delta位勢壘這位勢壘將一維空間分為兩個區域: 與 。在任何一個區域內,位勢為常數,薛丁格方程的解答可以寫為往右與往左傳播的波函式的疊加(參閱自由粒子):
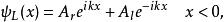 Delta位勢壘
Delta位勢壘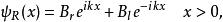 Delta位勢壘
Delta位勢壘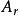 Delta位勢壘
Delta位勢壘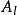 Delta位勢壘
Delta位勢壘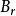 Delta位勢壘
Delta位勢壘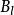 Delta位勢壘
Delta位勢壘 Delta位勢壘
Delta位勢壘 Delta位勢壘
Delta位勢壘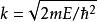 Delta位勢壘
Delta位勢壘其中, 、 、 、 都是必須由邊界條件決定的常數,下標 與 分別標記波函式往右或往左的方向。 是波數。
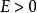 Delta位勢壘
Delta位勢壘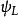 Delta位勢壘
Delta位勢壘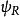 Delta位勢壘
Delta位勢壘 Delta位勢壘
Delta位勢壘由於 , 與 都是行進波。這兩個波必須滿足在 的邊界條件:
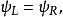 Delta位勢壘
Delta位勢壘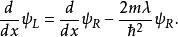 Delta位勢壘
Delta位勢壘 Delta位勢壘
Delta位勢壘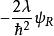 Delta位勢壘
Delta位勢壘特別注意第二個邊界條件方程,波函式隨位置的導數在 並不是連續的,在位勢壘兩邊的差額有 這么多。這方程的推導必須用到薛丁格方程。將薛丁格方程積分於{\displaystyle x=0\,\!}的一個非常小的鄰域:
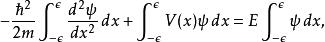 Delta位勢壘
Delta位勢壘 Delta位勢壘
Delta位勢壘其中, 是一個非常小的數值。
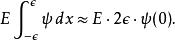 Delta位勢壘
Delta位勢壘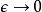 Delta位勢壘
Delta位勢壘在 的極限,這項目往著0去。
左邊是
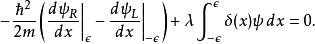 Delta位勢壘
Delta位勢壘根據狄拉克Delta函式的定義,
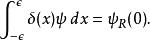 Delta位勢壘
Delta位勢壘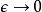 Delta位勢壘
Delta位勢壘而在 的極限,
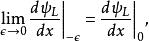 Delta位勢壘
Delta位勢壘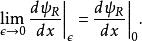 Delta位勢壘
Delta位勢壘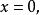 Delta位勢壘
Delta位勢壘稍加編排,可以得到第二個邊界條件方程:在
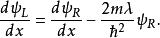 Delta位勢壘
Delta位勢壘從這兩個邊界條件方程。稍加運算,可以得到以下方程:
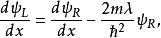 Delta位勢壘
Delta位勢壘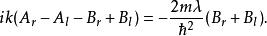 Delta位勢壘
Delta位勢壘反射與透射
 Delta位勢壘
Delta位勢壘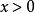 Delta位勢壘
Delta位勢壘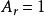 Delta位勢壘
Delta位勢壘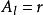 Delta位勢壘
Delta位勢壘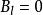 Delta位勢壘
Delta位勢壘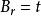 Delta位勢壘
Delta位勢壘 Delta位勢壘
Delta位勢壘 Delta位勢壘
Delta位勢壘由於能量是正值的,粒子可以自由的移動於位勢壘外的兩個半空間, 或 。可是,在Delta位勢壘,粒子會遇到散射狀況。設定粒子從左邊入射。在Delta位勢壘,粒子可能會被反射回去,或者會被透射過去。我們想要知道散射的反射係數與透射係數。設定 , , , 。求算反射的機率幅 與透射的機率幅 :
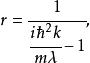 Delta位勢壘
Delta位勢壘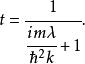 Delta位勢壘
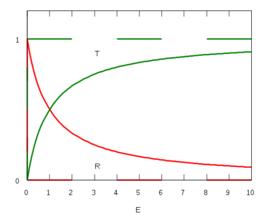
Delta位勢壘反射係數是
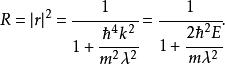 Delta位勢壘
Delta位勢壘透射係數是
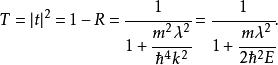 Delta位勢壘
Delta位勢壘這純粹是一個量子力學的效應,稱為量子隧穿效應;在經典力學裡,透射係數等於0,粒子不可能會透射過位勢壘。
•由於模型的對稱性,假若,粒子從右邊入射,我們也會得到同樣的答案。
•很奇異地,給予同樣的能量、質量、與狄拉克Delta函式的強度,Delta位勢壘與Delta位勢阱有同樣的反射係數與透射係數。
參閱
•自由粒子
•無限深方形阱
•有限深方形阱
•有限位勢壘
•球對稱位勢
•Delta位勢阱
•量子隧穿效應