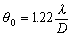存在的原因
我們在討論光學儀器的成像問題時，如果僅從幾何光學的定律來考慮，只要適當選擇透鏡焦距並適當安排多個透鏡的組合，總可能用提高放大率的辦法，把任何微小物體或遠處物體放大到清晰可見的程度。但通常光學儀器中所用的光闌和透鏡都是圓形的，它們是限制光束的孔徑，點光源發出的光通過透鏡時，光束受到限制的結果不是成點狀的像，而是經衍射成一明亮的圓斑（艾里斑）。
瑞利判據例如，遠方一顆星（可視為點光源）所發出的光，經望遠鏡的物鏡後所成的像，並不是幾何光學中的一點，而是一個有一定大小的衍射斑，該斑的大小與物鏡孔徑 ，光波長有關。當兩個星體過於靠近時，經物鏡所成的像斑之間的距離過近，大部分重疊在一起，這時兩個星體的像就難以分辨了。用顯微鏡觀察一個物體相距極近的兩點時，同樣會出現這種情況。
因此，實際光學儀器成像的清晰程度最終要受到光的衍射現象的限制。當放大率大到一定程度後，即使再增加放大率，儀器的分辨物體細節的性能也不會再提高了。也就是說，由於衍射的限制，光學儀器的解析度有一個最高的極限。
雖然光學儀器可以放大視角，從而使人能夠分辨物體的細節，但是不能用增大儀器的放大率來提高它的分辨本領。因為衍射效應給光學儀器分辨本領的限制。是不能用提高放大率的辦法來克服的。增大了放大率後。雖然放大了像點之間的距離，但每個像的衍射斑也同樣被放大了，所以光學儀器原來所不能分辨的東西，放得再大，仍不能為我們的眼睛或照相底片所分辨。
判定
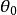最小分辨角對於一個光學儀器來說，如果一個點光源的衍射圖樣的中央最亮處剛好與一個點光源的衍射圖樣的第一個最暗處相重合，兩個像恰好能分辨，如圖 下圖（b)所示。我們稱為瑞利（Rayleigh）判據。恰能分辨的兩物點對透鏡光心的張角 叫做光學儀器的最小分辨角。
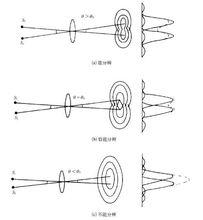光學儀器的分辨本領
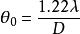最小分辨角根據瑞利判據，最小分辨角等於兩像斑中心的角距離，恰好等於艾里斑的半角寬度，因此，光學儀器的最小分辨角為 。
分辨本領
1.人眼的分辨本領：
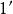最小分辨角物體發出的光線通過人眼的瞳孔，經人眼的折射系統成像於視網膜上。由於人眼的焦距只有 20mm左右，故視網膜上的像是夫琅禾費圓孔衍射圖樣。瞳孔基本上是圓孔，其直徑由虹膜在 2~8mm範圍內調節，在正常的光亮度條件下，瞳孔直徑大約為 3mm，人眼最敏感的綠光波長為 550nm，人眼的最小分辨角為 。
2.望遠鏡的分辨本領：
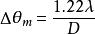最小分辨角望遠鏡的分辨本領望遠鏡的光學系統由物鏡和目鏡組成，遠方的物體經物鏡成像於它的第二焦平面上或焦平面附近。由於物體離物鏡很遠，物鏡接收的是近似平行光，故可認為是夫琅禾費圓孔衍射。若望遠鏡物鏡的直徑為 D，則它能分辨的最小角度，即分辨本領為 。
因此 ，要提高望遠鏡的分辨本領 ，就必須增大物鏡的直徑。
望遠鏡的目鏡不能提高它的分辨本領，只是讓物鏡的分辨本領得到了充分利用。這也同時說明，單純增大望遠鏡的目鏡的放大率並不能提高望遠鏡的分辨本領。因為增大了放大率，雖然像點之間的距離放大了，但每個像點的艾里斑也同樣被放大了，原來不能分辨的兩點，放得再大也還是不能分辨 。
3.顯微鏡的分辨本領：
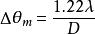最小分辨角對望遠鏡 、照相機等光學儀器，發光物體距成像透鏡均較遠，可視為夫琅禾費衍射。故這些光學儀器的分辨本領可由式 決定。但對於顯微鏡來說，由於物體距物鏡很近，此時已不是夫琅禾費衍射而是菲涅耳衍射 ，要精確計算顯微鏡的分辨本領非常複雜。但因物鏡的孔徑與像距相比很小，計算可得每一物點產生的艾里斑與平行光衍射產生的艾里斑的角半徑幾乎相同，故仍可用夫琅禾費圓孔衍射來討論顯微鏡的分辨本領。
由於目鏡只是對物鏡的像再次放大，不增加分辨本領，故顯微鏡的分辨本領也決定於物鏡的分辨本領。同樣道理，使用顯微鏡時也要注意放大率與分辨本領的匹配 。
