定義
最大熵譜估計是根據信號在已知有限延遲點上的自相關函式值保持不變,而按最大熵準則將未知延遲點的自相關函式進行外推後而獲其功率譜密度估計的方法。這種方法是一種可獲得高解析度的非線性譜估計方法,特別適用於短數據序列的譜估計。
熵在資訊理論中是反映信息度量的一個量。某隨機事件的隨機性越大,即不確定性越高,則熵值也越大,所攜帶的信息量亦越大。因此,根據熵量最大的準則,由已知自相關函式,外推未知自相關函式後獲得信號 譜估計,亦即可保證已知信息量不變化,而獲得估計已知信息量最大的一種譜估計方法。利用最大熵提高譜估計的解析度,獲得明顯的效果。
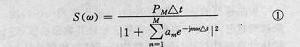 圖1 公式
圖1 公式最大熵功率譜估計表達式:若某隨機信號x(n)在時延為1到M點上的自相關函式值r(m)(m=l…M)為已知時,則其最大熵譜估計的表達式為圖1。
 圖3 公式
圖3 公式式中P為M階預測誤差濾波器的輸出功率;△t是抽樣周期;a(m=l,2…M)是模型參數,由圖2,3式決定。
式中的r(M)為已知的隨機過程的自相關函式值。
從最大熵功率譜估計的表達式可以看出,最大熵法與自回歸(AR)信號模型分析法以及線性預測誤差濾波法是等價的,只是從不同的觀點出發得到了相同的結果。
由已知信號計算功率譜估值的遞推算法 套用上述的譜估值表達式進行計算時,需要知道有限個自相關函式值。但是,實際的情況往往是只知道有限長的時間信號序列,而不知道其自相關函式值。為了解決這個問題,J.P.伯格提出了一種直接由已知時間信號序列計算功率譜估值的遞推算法,稱為伯格算法。因此使最大熵法得到廣泛的套用。
熵
在統計學中,熵是對各種隨機試驗不確定程度的一種度量。機率分布的熵越大、試驗的可能結果越不確定。伯格的思想是要在外推相關函式的每一步,都既能保證相關函式的已知部分不變,又能在新增加外推值之後使機率分布具有最大的熵;也就是在每步外推時不對未知點處自相關函式取值施加任何限制(即其取值具有最大統計自由度,不對它強加任何條件)。極大熵譜估計的這種特點能克服傳統的功率譜估計方法解析度不高的弱點。在理論上,過程的功率譜是自相關函式的傅立葉變換。傳統的功率譜估計方法是將樣本自相關函式乘以某種窗函式(即對自相關函式加權),然後再作傅立葉變換。窗函式可以增加譜估計的穩定性並減少譜的泄漏,但窗函式會限制譜的分辨力。傳統方法存在的問題實際上是由於它把沒有觀測到的數據(或其自相關函式)都看作為零,同時對已知部分的信息加以人為修改(加權)而引起的。而極大熵譜估計對已知的最大遲延以外的自相關函式進行合理的外推,因而能提高所求功率譜的分辨力,特別是在已知數據量較少時,其效果比傳統方法更優。
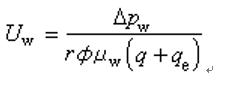 圖4 公式
圖4 公式假設一個平穩正態過程自相關函式的前N+1個遲延點的值r(0),r(1),…,r(N)已確知,需要求r(N+1)的值。以r(0),r(1),…,r(N+1)作為相關函式,則對應的N+2維常態分配的熵為圖4。
其中R(N+1)為相關陣。
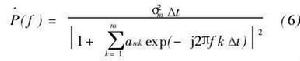 圖5 公式
圖5 公式因此使熵為最大就相當於使行列式 det【R(N+1)】為最大。可以使det【R(N+1)】對r(N+1)的偏導數為零,求出r(N+1)。將得到的r(N+1)代入R(N+2),同理可根據使det【R(N+2)】為最大的條件求出r(N+2)。再把求到的r(N+1)和r(N+2)代入R(N+3)中的相應元素,對det【R(N+3)】求極大可得到r(N+3),依此類推。與這種方法得到的自相關函式所對應的功率譜為圖5:
式中i=刧,Δt是x(t)的採樣間隔,ω為頻率,M+1為遞推次數,而A屌(a0,…,aM)T中各元素可由R(M)A=(1,0,…,0)T 求得,T表示轉置。 實際計算時,由於只掌握x(t)的有限記錄而無法得知自相關函式的精確值,因此只能用它的估計值替代。伯格在求取r和A(參數向量)的估值方面還提出一種遞推算法,它可以避免矩陣求逆,充分利用數據所提供的信息,而且遞推過程每步所對應的行列式detR都是非負定的。後來又有其他學者提出新的算法,克服伯格算法中的缺點(如所謂譜線分裂和譜峰漂移),但算法的變化並不改變極大熵的原則。
