基本介紹
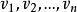 最優樹問題
最優樹問題 最優樹問題
最優樹問題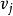 最優樹問題
最優樹問題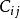 最優樹問題
最優樹問題假設要在n個城市 之間建一個公路網,使得這n個城市互通公路,已知連線城市 和 的公路造價為 ,要求設計一個總造價最小的公路網,這就是所謂連線問題。
從圖論角度看, 連線問題可敘述為:在一個賦權連通圖G中,找出一個具有最小權的連通子圖,顯然,它必是G的一個生成樹T,且權最小.我們稱這種樹為 最優樹 。
最優樹問題的解法
對於有限賦權圖,由於它的生成樹數目有限,因此,總可以通過逐個比較最終找到一個最優樹(可能不唯一),這說明最優樹是存在的,但當頂點和邊的數目較大時,這種方法顯然是不切實際的。Kruskal於1956年提出了求最優樹的有效算法,其步驟如下(設G的各邊權非負且無環):
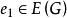 最優樹問題
最優樹問題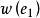 最優樹問題
最優樹問題(1)選擇 ,使權 最小;
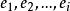 最優樹問題
最優樹問題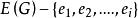 最優樹問題
最優樹問題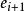 最優樹問題
最優樹問題(2)假設已選好 ,則從 中選取 滿足:
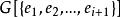 最優樹問題
最優樹問題① 無迴路;
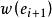 最優樹問題
最優樹問題② 是滿足①的儘可能小的權;
(3)重複(2)直到不存在滿足①的邊。
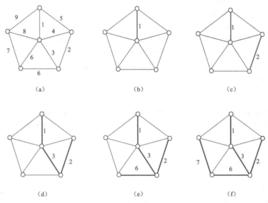
例如,圖1給出了利用上述算法求最優樹的過程,其中,粗邊就是算法所選定的邊 。
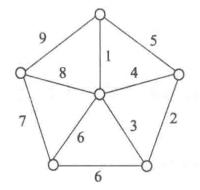 圖1(a) 圖1(a) | 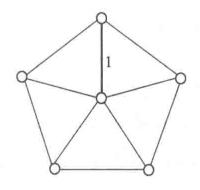 圖1(b) 圖1(b) | 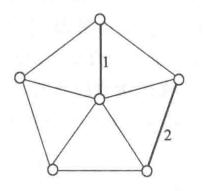 圖1(c) 圖1(c) |
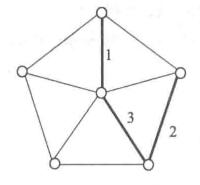 圖1(d) 圖1(d) | 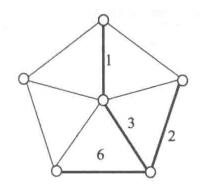 圖1(e) 圖1(e) | 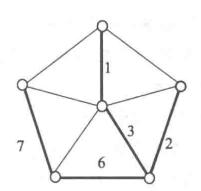 圖1(f) 圖1(f) |
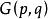 最優樹問題
最優樹問題定理1 設是一個圖,於是,下列說法相互等價:
(1)G是樹;
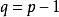 最優樹問題
最優樹問題(2)G連通且;
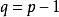 最優樹問題
最優樹問題(3)G無迴路且;
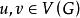 最優樹問題
最優樹問題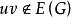 最優樹問題
最優樹問題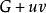 最優樹問題
最優樹問題(4)G無迴路,但對任意,若,則中恰有一條迴路;
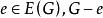 最優樹問題
最優樹問題(5)G是連通,但對任意不連通。
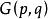 最優樹問題
最優樹問題定理2 對賦權G(P,q),用Kruskal算法得到G的子圖T*必是最優樹。
證明:首先,由Kruskal算法容易證明T*是G的生成樹。
設
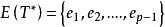 最優樹問題
最優樹問題對G的每個不同於T*的生成樹T,令
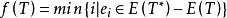 最優樹問題
最優樹問題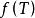 最優樹問題
最優樹問題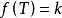 最優樹問題
最優樹問題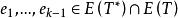 最優樹問題
最優樹問題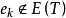 最優樹問題
最優樹問題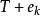 最優樹問題
最優樹問題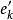 最優樹問題
最優樹問題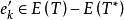 最優樹問題
最優樹問題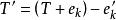 最優樹問題
最優樹問題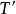 最優樹問題
最優樹問題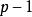 最優樹問題
最優樹問題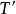 最優樹問題
最優樹問題假設T*不是最優樹,令T是使取最大值的最優樹,設,於是,,但。由定理1(4)知,中含唯一的迴路C。令是C中滿足的邊,作,於是是一個有條邊的連通圖,由定理1(2)知,是G的生成樹。顯然
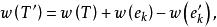 最優樹問題
最優樹問題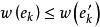 最優樹問題
最優樹問題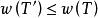 最優樹問題
最優樹問題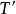 最優樹問題
最優樹問題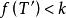 最優樹問題
最優樹問題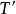 最優樹問題
最優樹問題而由算法知,,從而,這說明也是G的最優樹,但,,此與T的選取矛盾,故是最優樹。