介紹
CART是在給定輸入隨機變數X條件下輸出隨機變數Y的條件機率分布的學習方法。CART假設決策樹是二叉樹,內部結點特徵的取值為“是”和“否”,左分支是取值為“是”的分支,右分支是取值為“否”的分支。這樣的決策樹等價於遞歸地二分每個特徵,將輸入空間即特徵空間劃分為有限個單元,並在這些單元上確定預測的機率分布,也就是在輸入給定的條件下輸出的條件機率分布。
CART算法由以下兩步組成:
1) 樹的生成:基於訓練數據集生成決策樹,生成的決策樹要儘量大;
2) 樹的剪枝:用驗證數據集對已生成的樹進行剪枝並選擇最優子樹,這時損失函式最小作為剪枝的標準。
決策樹的生成就是通過遞歸地構建二叉決策樹的過程,對回歸樹用平方誤差最小化準則,對分類樹用基尼指數最小化準則,進行特徵選擇,生成二叉樹。
回歸樹的生成
假設X與Y分別是輸入和輸出向量,並且Y是連續變數,給定訓練數據集
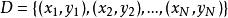 分類與回歸樹
分類與回歸樹考慮如何生成回歸樹。
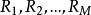 分類與回歸樹
分類與回歸樹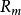 分類與回歸樹
分類與回歸樹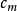 分類與回歸樹
分類與回歸樹一個回歸樹對應著輸入空間(即特徵空間)的一個劃分以及在劃分的但單元上的輸出值。假設已將輸入空間劃分為M個單元 ,並且在每個單元 上有一個固定的輸出值 ,於是回歸樹模型可表示為
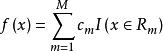 分類與回歸樹
分類與回歸樹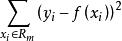 分類與回歸樹
分類與回歸樹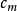 分類與回歸樹
分類與回歸樹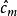 分類與回歸樹
分類與回歸樹 分類與回歸樹
分類與回歸樹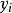 分類與回歸樹
分類與回歸樹當輸入空間的劃分確定時,可以用平方誤差 來表示回歸樹對於訓練數據的預測誤差,用平方誤差最小的準則求解每個單元上的最優輸出值。易知,單元 上的 的最優值 是 上所有輸入實例 對於的輸出 的均值,即
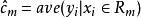 分類與回歸樹
分類與回歸樹 分類與回歸樹
分類與回歸樹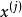 分類與回歸樹
分類與回歸樹 分類與回歸樹
分類與回歸樹問題是怎樣對輸入空間進行劃分,這裡採用啟發式的方法,選擇第 個變數 和它取的值 ,作為切分變數和切分點,並定義兩個區域:
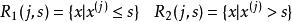 分類與回歸樹
分類與回歸樹 分類與回歸樹
分類與回歸樹然後尋找最優切分變數 和最優切分點 。具體的,求解
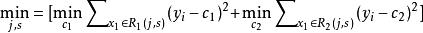 分類與回歸樹
分類與回歸樹 分類與回歸樹
分類與回歸樹 分類與回歸樹
分類與回歸樹對固定輸入變數 可以找到最優切分點
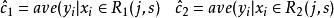 分類與回歸樹
分類與回歸樹 分類與回歸樹
分類與回歸樹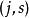 分類與回歸樹
分類與回歸樹遍歷所有輸入變數,找到最優切分變數 ,構成一個對 ,依次將輸入空間劃分為兩個區域。接著,每個對每個區域重複上述劃分過程,直到滿足停止條件為止。這樣就生成一棵回歸樹,這樣的回歸樹通常被稱為最小二乘樹。
分類樹的生成
分類樹用基尼指數選擇最優特徵,同時決定該特徵的最優二值切分點。
基尼指數
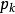 分類與回歸樹
分類與回歸樹在分類過程中,假設有K個類,樣本點屬於第k個類的機率為 ,則機率分布的基尼指數定義為:
對於二類分類問題,若樣本點屬於第1個類的機率是p,則機率分布的基尼指數為:
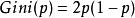 分類與回歸樹
分類與回歸樹對於給定的樣本集合D ,其基尼指數為:
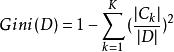 分類與回歸樹
分類與回歸樹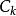 分類與回歸樹
分類與回歸樹其中, 是D中屬於第k類的樣本子集,K是類的個數。
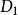 分類與回歸樹
分類與回歸樹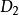 分類與回歸樹
分類與回歸樹如果樣本集合D根據特徵A是否取某一可能值a 被分割成 和 兩部分,即:
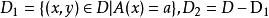 分類與回歸樹
分類與回歸樹則在特徵A的條件下,集合D的基尼指數定義為:
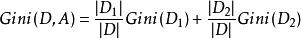 分類與回歸樹
分類與回歸樹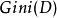 分類與回歸樹
分類與回歸樹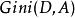 分類與回歸樹
分類與回歸樹基尼指數 表示集合D的不確定性,基尼指數 表示經A=a分割後集合D的不確定性。基尼指數越大,樣本集合的不確定性越大,這一點與熵相似。
生成算法
輸入:訓練數據集D,停止計算的條件
輸出:CART決策樹
根據訓練數據集,從根結點開始,遞歸地對每個結點進行以下操作,構建二叉決策樹:
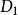 分類與回歸樹
分類與回歸樹(1)設結點的訓練數據集為D,計算現有特徵對該數據集的基尼係數。此時,對每個特徵A,對其可能取得每一個值a,根據樣本點A=a的測試為“是"或”否“將D分成 和 兩部分,計算A=a時的基尼指數
(2)在所有可能的特徵A以及它們所有可能的切分點a中,選擇基尼指數最小的特徵及其對應的切分點作為最優特徵與最優切分點,依據最優特徵與最優切分點,從現結點生成兩個子結點,將訓練數據集依特徵分配到兩個子結點中去
(3)對兩個子結點遞歸地調用 (1),(2),直至滿足停止條件
(4)生成CART決策樹
算法停止計算的條件是結點中的樣本個數小於預定的閾值,或樣本集的基尼指數小於預定的閾值(樣本基本屬於同一類),或者沒有更多特徵。
CART剪枝
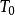 分類與回歸樹
分類與回歸樹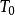 分類與回歸樹
分類與回歸樹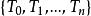 分類與回歸樹
分類與回歸樹CART剪枝算法從”完全生長“的決策樹的底端剪去一些子樹,使決策樹變小(模型變簡單),從而能夠對未知的數據有更準確的預測。CART剪枝算法由兩步組成:首先從生成算法產生決策樹 底端開始不斷剪枝,直到 的根結點,形成一個子序列 ;然後通過交叉驗證法在獨立的驗證數據集上對子樹序列進行測試,從中選擇最優子樹。
通過CART生成的樹,記為T,然後從T的底端開始剪枝,直到根節點。在剪枝的過程中,計算損失函式:
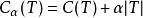 分類與回歸樹
分類與回歸樹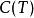 分類與回歸樹
分類與回歸樹, 為訓練數據的預測誤差, 為模型的複雜度。
 分類與回歸樹
分類與回歸樹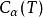 分類與回歸樹
分類與回歸樹 分類與回歸樹
分類與回歸樹 分類與回歸樹
分類與回歸樹 分類與回歸樹
分類與回歸樹 分類與回歸樹
分類與回歸樹對於一個固定的 ,在T中一定存在一顆樹 使得損失函式 最小。也就是每一個固定的 ,都存在一顆相應的使得損失函式最小的樹。這樣不同的 會產生不同的最優樹,而我們不知道在這些最優樹中,到底哪顆最好,於是我們需要將 在其取值空間內劃分為一系列區域,在每個區域都取一個 然後得到相應的最優樹,最終選擇損失函式最小的最優樹。
 分類與回歸樹
分類與回歸樹現在對 取一系列的值,分別為:
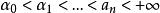 分類與回歸樹
分類與回歸樹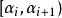 分類與回歸樹
分類與回歸樹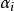 分類與回歸樹
分類與回歸樹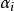 分類與回歸樹
分類與回歸樹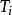 分類與回歸樹
分類與回歸樹產生一系列的區間 。在每個區間內取一個值 ,對每個 ,我們可以得到一顆最優樹 。於是我們得到一個最優樹列表{T0,T1,…,Tn}。
 分類與回歸樹
分類與回歸樹那么對於一個固定的 ,如何找到最優的子樹?
現在假如節點t就是一棵樹,一顆單節點的樹,則其損失函式為:
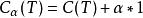 分類與回歸樹
分類與回歸樹對於一個以節點t為根節點的樹,其損失函式為:
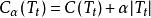 分類與回歸樹
分類與回歸樹 分類與回歸樹
分類與回歸樹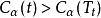 分類與回歸樹
分類與回歸樹當 =0時,即沒有剪枝時, 。
 分類與回歸樹
分類與回歸樹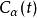 分類與回歸樹
分類與回歸樹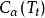 分類與回歸樹
分類與回歸樹然而,隨著 的增大, 和 的大小關係會出現變化。
當Ca(t)= Ca(T)時,即:
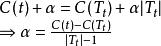 分類與回歸樹
分類與回歸樹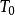 分類與回歸樹
分類與回歸樹 分類與回歸樹
分類與回歸樹 分類與回歸樹
分類與回歸樹 分類與回歸樹
分類與回歸樹 分類與回歸樹
分類與回歸樹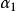 分類與回歸樹
分類與回歸樹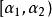 分類與回歸樹
分類與回歸樹據上分析,在 中的每個內部節點,計算 的值,它表示剪枝後整體損失函式減少的程度。在T0中剪去 最小的子樹T,將得到的新的樹記為 ,同時將此 記為 。即 為區間上的最優樹。
 分類與回歸樹
分類與回歸樹 分類與回歸樹
分類與回歸樹 分類與回歸樹
分類與回歸樹 分類與回歸樹
分類與回歸樹 分類與回歸樹
分類與回歸樹 分類與回歸樹
分類與回歸樹與損失函式之間的關係分析:當 =0時,此時未進行任何剪枝,因為產生過擬合,所以損失函式會較大,而隨著的增大,產生的過擬合會慢慢消退,因而,損失函式會慢慢減小,當增大到某一值時,損失函式會出現一個臨界值,因而超過此臨界值繼續增大的話損失函式就會因而模型越來越簡單而開始增大。所以我們需要找到一個使損失函式最小的臨界點。
 分類與回歸樹
分類與回歸樹如何找到使損失函式最小的呢?
 分類與回歸樹
分類與回歸樹 分類與回歸樹
分類與回歸樹 分類與回歸樹
分類與回歸樹 分類與回歸樹
分類與回歸樹 分類與回歸樹
分類與回歸樹依次遍歷生成樹的每一個內部節點,分別計算剪掉該內部節點和不剪掉該內部節點時的整體損失函式,當這兩種情況的損失函式相等時,我們可以得到一個,此表示當前需要剪枝的最小。這樣每個內部節點都能計算出一個。此示整體損失函式減少的程度。
 分類與回歸樹
分類與回歸樹那么選擇哪個來對生成樹進行剪枝呢?
 分類與回歸樹
分類與回歸樹 分類與回歸樹
分類與回歸樹 分類與回歸樹
分類與回歸樹我們選擇上面計算出的最小的來進行剪枝。假如我們選擇的不是最小的進行剪枝的話,則至少存在兩處可以剪枝的內部節點,這樣剪枝後的損失函式必然會比只剪枝一處的損失要大(這句話表述的可能不準確),為了使得損失函式最小,因而選最小的來進行剪枝。
 分類與回歸樹
分類與回歸樹 分類與回歸樹
分類與回歸樹在選出之後,我們就需要計算該對應的使損失函式最小的子樹。即從樹的根節點出發,逐層遍歷每個內部節點,計算每個內部節點處是否需要剪枝。剪枝完之後的樹便是我們所需要的樹。
