旅行商問題
 旅行商問題
旅行商問題旅行商問題(TravelingSalemanProblem,TSP)又譯為旅行推銷員問題、貨郎擔問題,簡稱為TSP問題,是最基本的路線問題,該問題是在尋求單一旅行者由起點出發,通過所有給定的需求點之後,最後再回到原點的最小路徑成本。最早的旅行商問題的數學規劃是由Dantzig(1959)等人提出。
簡介
“旅行商問題”常被稱為“旅行推銷員問題”,是指一名推銷員要拜訪多個地點時,如何找到在拜訪每個地點一次後再回到起點的最短路徑。規則雖然簡單,但在地點數目增多後求解卻極為複雜。以42個地點為例,如果要列舉所有路徑後再確定最佳行程,那么總路徑數量之大,幾乎難以計算出來。多年來全球數學家絞盡腦汁,試圖找到一個高效的算法,近來在大型計算機的幫助下才取得了一些進展。
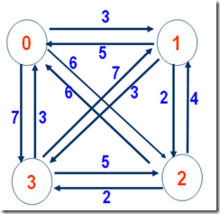 TSP問題
TSP問題TSP問題在物流中的描述是對應一個物流配送公司,欲將n個客戶的訂貨沿最短路線全部送到。如何確定最短路線。
TSP問題最簡單的求解方法是枚舉法。它的解是多維的、多局部極值的、趨於無窮大的複雜解的空間,搜尋空間是n個點的所有排列的集合,大小為(n-1)。可以形象地把解空間看成是一個無窮大的丘陵地帶,各山峰或山谷的高度即是問題的極值。求解TSP,則是在此不能窮盡的丘陵地帶中攀登以達到山頂或谷底的過程。
研究歷史
旅行商問題字面上的理解是:有一個推銷員,要到n個城市推銷商品,他要找出一個包含所有n個城市的具有最短路程的環路。TSP的歷史很久,最早的描述是1759年歐拉研究的騎士週遊問題,即對於西洋棋棋盤中的64個方格,走訪64個方格一次且僅一次,並且最終返回到起始點。TSP由美國RAND公司於1948年引入,該公司的聲譽以及線性規劃這一新方法的出現使得TSP成為一個知名且流行的問題。
問題解法
旅行推銷員的問題,我們稱之為巡行(Tour),此種問題屬於NP-Complete的問題,所以旅行商問題大多集中在啟發式解法。Bodin(1983)等人將旅行推銷員問題的啟發式解法分成三種:
1、途程建構法(TourConstructionProcedures)
從距離矩陣中產生一個近似最佳解的途徑,有以下幾種解法:
1)最近鄰點法(NearestNeighborProcedure):一開始以尋找離場站最近的需求點為起始路線的第一個顧客,此後尋找離最後加入路線的顧客最近的需求點,直到最後。
2)節省法(ClarkandWrightSaving):以服務每一個節點為起始解,根據三角不等式兩邊之和大於第三邊之性質,其起始狀況為每服務一個顧客後便回場站,而後計算路線間合併節省量,將節省量以降序排序而依次合併路線,直到最後。
3)插入法(Insertionprocedures):如最近插入法、最省插入法、隨意插入法、最遠插入法、最大角度插入法等。
2、途程改善法(TourImprovementProcedure)
先給定一個可行途程,然後進行改善,一直到不能改善為止。有以下幾種解法:
1)K-Opt(2/3Opt):把尚未加入路徑的K條節線暫時取代目前路徑中K條節線,並計算其成本(或距離),如果成本降低(距離減少),則取代之,直到無法改善為止,K通常為2或3。
2)Or-Opt:在相同路徑上相鄰的需求點,將之和本身或其它路徑交換且仍保持路徑方向性,並計算其成本(或距離),如果成本降低(距離減少),則取代之,直到無法改善為止。
3、合成啟發法(CompositeProcedure)
先由途程建構法產生起始途程,然後再使用途程改善法去尋求最佳解,又稱為兩段解法(twophasemethod)。有以下幾種解法:
1)起始解求解+2-Opt:以途程建構法建立一個起始的解,再用2-Opt的方式改善途程,直到不能改善為止。
2)起始解求解+3-Opt:以途程建構法建立一個起始的解,再用3-Opt的方式改善途程,直到不能改善為止。
解法思路
旅行推銷員的問題,我們稱之為巡行(Tour),此種問題屬於NP-Complete的問題,所以旅行商問題大多集中在啟發式解法。Bodin(1983)等人將旅行推銷員問題的啟發式解法分成三種:
途程建構法
從距離矩陣中產生一個近似最佳解的途徑,有以下幾種解法:
1、最近鄰點法(NearestNeighborProcedure):一開始以尋找離場站最近的需求點為起始路線的第一個顧客,此後尋找離最後加入路線的顧客最近的需求點,直到最後。
2、節省法(ClarkandWrightSaving):以服務每一個節點為起始解,根據三角不等式兩邊之和大於第三邊之性質,其起始狀況為每服務一個顧客後便回場站,而後計算路線間合併節省量,將節省量以降序排序而依次合併路線,直到最後。
3、插入法(Insertionprocedures):如最近插入法、最省插入法、隨意插入法、最遠插入法、最大角度插入法等。
途程改善法
先給定一個可行途程,然後進行改善,一直到不能改善為止。有以下幾種解法:
1、K-Opt(2/3Opt):把尚未加入路徑的K條節線暫時取代目前路徑中K條節線,並計算其成本(或距離),如果成本降低(距離減少),則取代之,直到無法改善為止,K通常為2或3。
2、Or-Opt:在相同路徑上相鄰的需求點,將之和本身或其它路徑交換且仍保持路徑方向性,並計算其成本(或距離),如果成本降低(距離減少),則取代之,直到無法改善為止。
合成啟發法
先由途程建構法產生起始途程,然後再使用途程改善法去尋求最佳解,又稱為兩段解法(twophasemethod)。有以下幾種解法:
1、起始解求解+2-Opt:以途程建構法建立一個起始的解,再用2-Opt的方式改善途程,直到不能改善為止。
2、起始解求解+3-Opt:以途程建構法建立一個起始的解,再用3-Opt的方式改善途程,直到不能改善為止。
研究進展
 小蜜蜂解決大問題
小蜜蜂解決大問題2010年10月25日,英國一項最新研究說,在花叢中飛來飛去的小蜜蜂顯示出了輕易破解“旅行商問題”的能力,而這是一個吸引全世界數學家研究多年的大問題,如能理解蜜蜂的解決方式,將有助於人們改善交通規劃和物流等領域的工作。英國倫敦大學皇家霍洛韋學院等機構研究人員報告說,小蜜蜂顯示出了輕而易舉破解這個問題的能力。他們利用人工控制的假花進行了實驗,結果顯示,不管怎樣改變花的位置,蜜蜂在稍加探索後,很快就可以找到在不同花朵間飛行的最短路徑。這是首次發現能解決這個問題的動物,研究報告即將發表在《美國博物學家》雜誌上。進行研究的奈傑爾·雷恩博士說,蜜蜂每天都要在蜂巢和花朵間飛來飛去,為了采蜜而在不同花朵間飛行是一件很耗精力的事情,因此實際上蜜蜂每天都在解決“旅行商問題”。儘管蜜蜂的大腦只有草籽那么大,也沒有電腦的幫助,但它已經進化出了一套很好的解決方案,如果能理解蜜蜂怎樣做到這一點,對人類的生產、生活將有很大幫助。據介紹,“旅行商問題”的套用領域包括:如何規劃最合理高效的道路交通,以減少擁堵;如何更好地規劃物流,以減少運營成本;在網際網路環境中如何更好地設定節點,以更好地讓信息流動等。
問題分析
旅行商問題要從圖G的所有週遊路線中求取最小成本的週遊路線,而從初始點出發的週遊路線一共有(n-1)!條,即等於除初始結點外的n-1個結點的排列數,因此旅行商問題是一個排列問題。排列問題比子集合的選擇問題通常要難於求解得多,這是因為n個物體有n!種排列,只有個子集合(n!>O())。通過枚舉(n-1)!條週遊路線,從中找出一條具有最小成本的週遊路線的算法,其計算時間顯然為O(n!)。
枚舉法思想:程式中採用深度優先策略。(採用隱式和顯式兩種形式)
枚舉算法的特點是算法簡單,但運算量大,當問題的規模變大,循環的階數越大,執行的速度越慢。如果枚舉範圍太大(一般以不超過兩百萬次為限),在時間上就難以承受。在解決旅行商問題時,以頂點1為起點和終點,然後求{2…N}的一個全排列,使路程1→{2…N}的一個全排列→1上所有邊的權(代價)之和最小。所有可能解由(2,3,4,…,N)的不同排列決定。
為便於討論,介紹一些關於解空間樹結構的術語。在下面分析回溯法和分支限界法時都直接或間接用到解空間樹。在解空間樹中的每一個結點確定所求問題的一個問題狀態(problemstate)。由根結點到其它結點的所有路徑則確定了這個問題的狀態空間(statespace)。解狀態(solutionstates)表示一些問題狀態S,對於這些問題狀態,由根到S的那條路徑確定了這解空間中的一個元組。答案狀態(answerstates)表示一些解狀態S,對於這些解狀態而言,由根到S的這條路徑確定了這問題的一個解(即,它滿足隱式約束條件)。解空間的樹結構稱為狀態空間樹(statespacetree)。
對於旅行商問題,一旦構想出一種狀態空間樹,那么就可以先系統地生成問題狀態,接著確定這些問題狀態中的哪些狀態是解狀態,最後確定哪些解狀態是答案狀態,從而將問題解出。為了生成問題狀態,採用兩種根本不同的方法。如果已生成一個結點而它的所有兒子結點還沒有全部生成,則這個結點叫做活結點。當前正在生成其兒子結點的活結點叫E-結點。不再進一步擴展或者其兒子結點已全部生成的生成結點就是死結點。在生成問題狀態的兩種方法中,都要用一張活結點表。在第一種方法中,當前的E-結點R一旦生成一個新的兒子C,這個兒子結點就變成一個新的E-結點,當完全檢測了子樹C之後,R結點就再次成為E-結點。這相當與問題狀態的深度優先生成。在第二種狀態生成方法中,一個E-結點一直保持到死結點為止。這兩種方法中,將用限界函式去殺死還沒有全部生成其兒子結點的那些活結點。如果旅行商問題要求找出全部解,則要生成所有的答案結點。使用限界函式的深度優先結點生成方法稱為回溯法。E-結點一直保持到死為止的狀態生成方法稱為分支限界法。
回溯法思想
為了套用回溯法,所要求的解必須能表示成一個n-元組(x1,…,Xn),其中x1是取自某個有窮集Si。通常,所求解的問題需要求取一個使某一規範函式P(x1,…,Xn)取極大值(或取極小值或滿足該規範函式條件)的向量。
假定集合Si的大小是mi,於是就有m=m1m2…Mn個n-元組可能滿足函式P。所謂硬性處理是構造這m個n-元組並逐一測試它們是否滿足P,從而找出該問題的所有最優解。而回溯法的基本思想是,不斷地用修改過的函式Pi(x1,…Xi)(即限界函式)去測試正在構造中的n-元組的部分向量(x1,…,Xi),看其是否可能導致最優解。如果判定(x1,…,Xi)不可能導致最優解,那么就可能要測試的後n-i個元素組成的向量一概略去。因此回溯法作的次數比硬性處理作的測試次數(m次)要少得多。用回溯法求解的旅行商問題,即在枚舉法的基礎上多了一個約束條件,約束條件可以分為兩種類型:顯示約束和隱式約束。
分支限界法思想:本題採用FIFO分支限界法。
如前所述,分支限界法是在生成當前E-結點全部兒子之後再生成其它活結點的兒子,且用限界函式幫助避免生成不包含答案結點子樹的狀態空間的檢索方法。在總的原則下,根據對狀態控制項樹中結點檢索的次序的不同又將分支限界設計策路分為數種不同的檢索方法。在求解旅行商問題時,程式中採用FIFO檢索(FirstInFirstOut),它的活結點表採用一張先進先出表(即佇列)。可以看出,分支限界法在兩個方面加速了算法的搜尋速度,一是選擇要擴展的節點時,總是選擇選擇一個最小成本的結點,儘可能早的進入最有可能成為最優解的分支;二是擴展節點的過程中,捨棄導致不可行解或導致非最優解的子結點。
貪心法思想
貪心法是一種改進了的分級處理方法。它首先旅行商問題描述,選取一種度量標準。然後按這種度量標準對n個輸入城市排序,並按序一次輸入一個城市。如果這個輸入和當前已構成在這種量度意義下的部分最優解加在一起不能產生一個可行解,則不把這個城市加入到這部分解中。這種能夠得到某種量度意義下的最優解的分級處理方法成為貪心方法。
獲得最優路徑的貪心法應一條邊一條邊地構造這棵樹。根據某種量度來選擇將要計入的下一條邊。最簡單的量度標準是選擇使得迄今為止計入的那些邊的成本的和有最小增量的那條邊。
