基本介紹
設有p個城鎮,已知每兩個城鎮之間的距離,一個售貨員從某一城鎮出發巡迴售貨,問這個售貨員應如何選擇路線,能使每個城鎮經過一次且僅一次,最後返回到出發地,而使總的行程最短?這個問題稱為 旅行售貨員問題。容易看出,旅行售貨員問題就是在一個賦權完全圖中找一個具有最小權的Hamilton圈,我們稱這種圈為最優Hamilton圈。
除旅行售貨員問題之外,郵局中負責到各個信箱取信的郵遞員,以及去各個分局送郵件的汽車等都會類似遇到這種問題,還有一些問題表面上似乎與之無關,而實質上卻可以歸結為旅行售貨員問題來解決,既然這個問題有著如此廣泛的套用,那么找一個求解最優Hamilton圈的有效算法就成為一件非常重要的事 。
問題解法
目前還沒有一個求解最優Hamilton圈的有效算法,所以希望有一個方法以獲得相當好(但不一定是最優)的解,下而我們給出一個較好的近似算法—— 最鄰近算法,以及一個修改的方法。
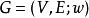 旅行售貨員問題
旅行售貨員問題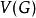 旅行售貨員問題
旅行售貨員問題 旅行售貨員問題
旅行售貨員問題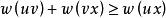 旅行售貨員問題
旅行售貨員問題設是一個賦權完全圖,根據實際問題,我們可作如下的規定:對中任何三個頂點,滿足。
求近似最優Hamilton圈的最鄰近算法:
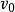 旅行售貨員問題
旅行售貨員問題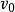 旅行售貨員問題
旅行售貨員問題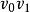 旅行售貨員問題
旅行售貨員問題(1) 任選一個頂點作為起點,找一條與關聯其權最小的一條邊e,e的另一個端點記為v,得一條路;
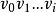 旅行售貨員問題
旅行售貨員問題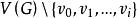 旅行售貨員問題
旅行售貨員問題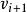 旅行售貨員問題
旅行售貨員問題 旅行售貨員問題
旅行售貨員問題(2)設已選出路,在中取一個與v最近的相鄰頂點,得;
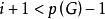 旅行售貨員問題
旅行售貨員問題 旅行售貨員問題
旅行售貨員問題(3)若,用i代i+i返回(2),否則記,停止。
最後所得的C就是G的一個近似最優的Hamilton圈。
例如,在圖1中,粗邊表示了起點選a並用最鄰近法求得的一個Hamilton圈C=adbcea,該Hamilton圈的長度為40。
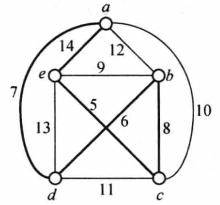 圖1 圖G的一個Hamilton圈C
圖1 圖G的一個Hamilton圈C用最鄰近法求得的Hamilton圈一般不是最優的,但通過以下的修改可獲得更短的Hamilton圈,其修改方法如下:
 旅行售貨員問題
旅行售貨員問題 旅行售貨員問題
旅行售貨員問題設是G的一個Hamilton圈,若存在i,j適合,並且
 旅行售貨員問題
旅行售貨員問題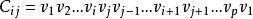 旅行售貨員問題
旅行售貨員問題 旅行售貨員問題
旅行售貨員問題 旅行售貨員問題
旅行售貨員問題 旅行售貨員問題
旅行售貨員問題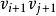 旅行售貨員問題
旅行售貨員問題則Hamilton圈(它是由C中刪去邊和,添加邊和而得到的(如圖2所示))的權和
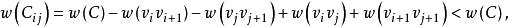 旅行售貨員問題
旅行售貨員問題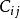 旅行售貨員問題
旅行售貨員問題因而Hamilton圈將是C的一個改進。
 圖2修改Hamilton圈的圖示圖
圖2修改Hamilton圈的圖示圖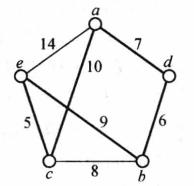 圖3 H-圈C=adbcea的一個修改方法
圖3 H-圈C=adbcea的一個修改方法在接連進行上述的一系列修改後,最後得到的一個Hamilton圈不能再用此方法改進了,這個Hamilton圈雖然未必是最優的,但有理由認為它常常是比較好的 。
例如,用最鄰近法得到的圖1所示的G的Hamilton圈為C=adbcea,用此方法修改後可得C'= acebda(見圖3),其長度為37。
我們可以利用Kruskal算法給出最優Hamilton圈下界的一個估計式,設v是賦權完全圖G的任意一個頂點,用Kruskal算法求出G-v的一棵最優樹T,設C是G的一個最優Hamilton圈,顯然C-v是G-v的一棵生成樹,因此
 旅行售貨員問題
旅行售貨員問題設G中與v關聯且權最小和權次小的兩條邊分別是e和f,則
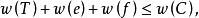 旅行售貨員問題
旅行售貨員問題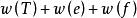 旅行售貨員問題
旅行售貨員問題因此將是G的最優Hamilton圈的一個下界估計式。以圖1中的G為例,G-c的圖為圖4(a)所示,用Kruskal算法求得G-c的一棵最優樹T(如圖4(b)所示),T的權為22,G中與c關聯而權最小的兩條邊為ce和西cb,因此G的最優Hamilton圈C滿足
 旅行售貨員問題
旅行售貨員問題 圖4(a)
圖4(a)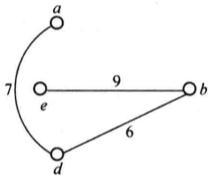 圖4(b)
圖4(b)由此可見,結合上面兩個方法所得到的Hamilton圈是一個較好的近似解,其實C'就是圖1所示的圖G的一個最優Hamilton圈 。

