定義
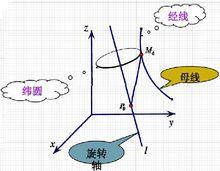 圖1
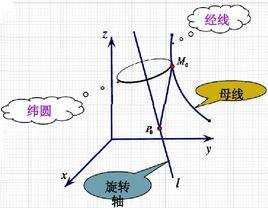
圖1定義:如圖1所示,在空間,一條曲線Г繞著定直線 l旋轉一周所生成的曲面叫做旋轉曲面,或稱迴轉曲面。曲線Г叫做旋轉曲面的母線,定直線 l 叫做旋轉曲面的旋轉軸,簡稱為軸。母線上任意一點繞旋轉軸旋轉的軌跡是一個圓,稱為旋轉曲面的緯圓或緯線。以旋轉軸為邊界的半平面與旋轉曲面的交線稱為旋轉曲面的經線。
說明:
(1)緯圓也可以看作垂直於旋轉軸的平面與旋轉曲面的交線;
(2)旋轉曲面可由母線繞旋轉軸旋轉生成,也可以由緯圓族生成,軸則是緯圓族的連心線;
(3)任一經線都可以作為母線,但母線不一定是經線。
曲面方程
求旋轉曲面的方程
如圖1所示,在空間直角坐標系下,設旋轉曲面的母線為:
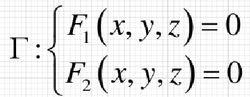 旋轉曲面
旋轉曲面旋轉軸為直線:
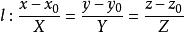 旋轉曲面
旋轉曲面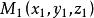 旋轉曲面
旋轉曲面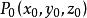 旋轉曲面
旋轉曲面設點 為Г上任意一點, 為 l 上任意一點。
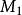 旋轉曲面
旋轉曲面過 的緯圓方程為:
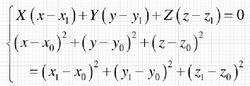 旋轉曲面
旋轉曲面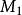 旋轉曲面
旋轉曲面又因為 在母線上,滿足母線的方程,有:
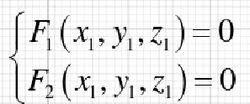 旋轉曲面
旋轉曲面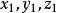 旋轉曲面
旋轉曲面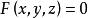 旋轉曲面
旋轉曲面聯立上述兩個方程組消去參數 ,最後得一個三元方程 ,即為以Г為母線, l 為旋轉軸的旋轉曲面的方程。
旋轉曲面方程
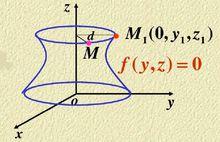 圖2
圖2設在yoz面上的一條已知曲線C,它的方程為:
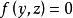 旋轉曲面
旋轉曲面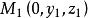 旋轉曲面
旋轉曲面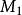 旋轉曲面
旋轉曲面曲線C繞z軸旋轉一周,得旋轉曲面,旋轉過程如圖2所示。設 是曲線C上任一點,M(x,y,z)是點 繞z軸旋轉所得的任一點,則:
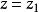 旋轉曲面
旋轉曲面(1) ;
(2) 點M(x, y, z)到z軸的距離為:
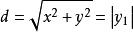 旋轉曲面
旋轉曲面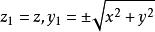 旋轉曲面
旋轉曲面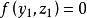 旋轉曲面
旋轉曲面將 代入曲線C的方程 ,得旋轉曲面的方程為:
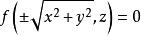 旋轉曲面
旋轉曲面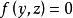 旋轉曲面
旋轉曲面該方程就是yoz坐標面上的已知曲線 繞z軸旋轉一周的旋轉曲面方程。
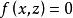 旋轉曲面
旋轉曲面同理,xoz坐標面上的已知曲線 繞y軸旋轉一周的旋轉曲面方程為:
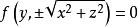 旋轉曲面
旋轉曲面特殊旋轉曲面
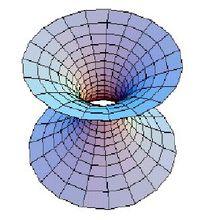 旋轉曲面
旋轉曲面旋轉雙曲面對於雙曲線:
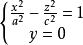 旋轉曲面
旋轉曲面繞z軸旋轉,得旋轉曲面:
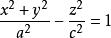 旋轉曲面
旋轉曲面繞x軸旋轉,得旋轉曲面:
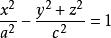 旋轉曲面
旋轉曲面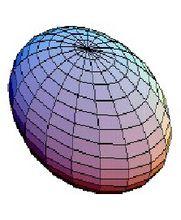 旋轉曲面
旋轉曲面旋轉橢球面對於橢圓:
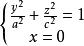 旋轉曲面
旋轉曲面繞y軸旋轉,得旋轉曲面:
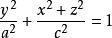 旋轉曲面
旋轉曲面繞z軸旋轉,得旋轉曲面:
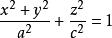 旋轉曲面
旋轉曲面旋轉拋物面對於拋物線:
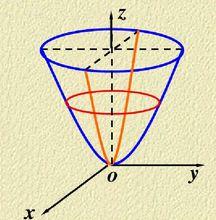 旋轉曲面
旋轉曲面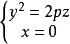 旋轉曲面
旋轉曲面繞z軸旋轉,得旋轉曲面:
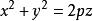 旋轉曲面
旋轉曲面面積計算
旋轉曲面的面積
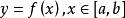 旋轉曲面
旋轉曲面設平面光滑曲線 C 的方程為 (不妨設f(x) ≥0)這段曲線繞 x 軸旋轉一周得到旋轉曲面,如圖3所示。則旋轉曲面的面積公式為:
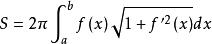 旋轉曲面
旋轉曲面如果光滑曲線 C 由參數方程:
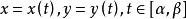 旋轉曲面
旋轉曲面給出,且 y(t) ≥0,那么由弧微分知識推知曲線 C 繞 x 軸旋轉所得旋轉曲面的面積為 :
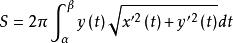 旋轉曲面
旋轉曲面創建旋轉曲面
用CAD模組中的工具,畫一條截面線以及用於確定旋轉軸的兩個標誌可以產生一個旋轉曲面。選擇的次序為先選截面線,再選標誌點,然後再點擊創建旋轉面圖示,螢幕上彈出創建旋轉曲面對話框。通過使用預設項,將產生上半個旋轉曲面。點擊對話框中所需按鈕來產生下半個,左半個或右半個,或者整個旋轉曲面。(以360°整個曲面表示)。您也能製作一個局部旋轉的曲面,在對話框中點擊這個圖示:輸入曲面的起始角度及終止角度。
例如:
1/2凹面: 180° 到 0°
1/2凸面: -180°到 0°