簡單介紹
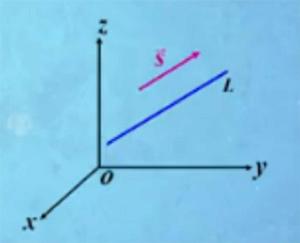
如果一個非零向量平行於一條已知直線,這個向量就叫做這條直線的方向向量。
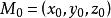 方向數
方向數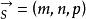 方向數
方向數由於過空間一點可作而且只能作一條直線平行於一已知直線,所以當直線L上一點和它的一方向向量 為已知時,直線L的位置就完全確定了。
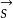 方向數
方向數直線的任一方向向量 的坐標m、n、p叫做這直線的一組方向數。
當方向數沒能對應在正方體或者長方體上面,而是在三維坐標圖中時,可以自己想像一個長方體出來,其長、寬、高就是{長,寬,高},這個表達形式就是方向數。把長寬高的平方和開方,得到的就是這個方向數的長度,既長方體的立體對角線。
方向數與方向餘弦
方向數、方向餘弦可以用來確定空間有向直線的方向,但是如果只需要確定一條空間直線的方位(一條直線的兩個方向均確定著同一方位),那末就不一定需要知道方向餘弦,而只要知道與方向餘弦成比例的三個數就可以了。這三個與方向餘弦成比例且不全為零的數A,B,C稱為空間直線的方向數,記作:{A,B,C},即:
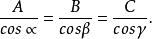 方向數
方向數據此可得到方向餘弦與方向數的轉換公式:
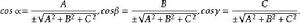 方向數
方向數其中,根式取正負號分別得到兩組方向餘弦,它們代表兩個相反的方向。
關於方向數的問題
空間任意兩點坐標之差就是聯結此兩點直線的一組方向數。
方向數求夾角
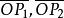 方向數
方向數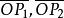 方向數
方向數設L1與L2是空間的任意兩條直線,它們可能相交,也可能不相交。通過原點O作平行與兩條直線的線段 ,則線段 的夾角稱為此兩直線L1與L2的夾角。
若知道L1與L2的方向數,則有公式為:
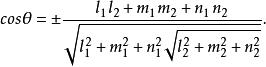 方向數
方向數方向數判別兩直線平行、垂直
兩直線平行的充分必要條件為:
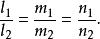 方向數
方向數兩直線平行的充分必要條件為:
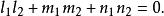 方向數
方向數方向數和方向向量的關係
方向數是方向向量在相應坐標軸上的投影,或者說方向數是方向向量的數字描述。方向數是指坐標向量的數據,如:向量a=(1,2),而方向向量也可能是非坐標向量下的向量。方向數一定是方向向量,但方向向量不一定是方向數。
例如:過點M(1,3,5)且方向數為{2,1,2}的直線方程為(x-1)/2=(y-3)/1=(x-5)/2;這條直線與向量a=2i+j+2k平行。另外,也可作圖驗證:畫個立體直角坐標,畫出點A(2,1,2),連線OA,這就是所求直線的方向向量a;再畫出點M(1,3,5);再任取m=1,算出x=2m+1=3,y=m+3=4,z=2m+5=7,畫出
點N(3,4,7),再連線MN。最後觀察出MN與OA平行。