斜堆的優勢是其合併的速度遠遠大於二叉堆。
斜堆是一種自適應的左偏樹。
定義
斜堆可遞歸的定義如下:
● 只有一個元素的堆是斜堆。
● 兩個斜堆通過斜堆的合併操作,得到的結果仍是斜堆。
操作
合併我們可以用左偏樹的合併算法實現兩個斜堆的合併。
除此之外,還有一種非遞歸的算法。
● 分割每個堆。方法是從根節點開始,右子樹與根節點分離,然後右子樹以同樣的方式分割。
最後得到一個樹的集合,集合中的樹的特點是:其根節點只有左子樹或者沒有子樹。
● 對集合中的樹,按照根節點的值從小到大排序。
● 從右到左,不斷地合併最後兩個子樹,直到只剩下一棵樹。
合併方法是:
● 如果倒數第二棵樹有左子樹,那么把左子樹變為右子樹。
● 把最後一棵樹作為倒數第二棵樹的左子樹。 合併的時間複雜度分析 :斜堆合併的攤還時間為O(logN)
定義:一個節點p,若其右子樹的後裔數至少是p的後裔數的一般,則稱p是重節點,否則稱為輕節點
位勢的選取:右路徑上重節點的數目
證明:
令H1和H2為兩個斜堆,節點數為N1和N2,右路徑上輕重節點數目分別為l1和h1、 l2和h2
若合併代價定義為右路徑上節點總數,則代價為l1+h1+l2+h2
合併操作的重要特性:右路徑上的重節點肯定變為輕節點;而輕節點可能不變,也可能變為重節點。
考慮最壞情況,當然是所有輕節點均變為重節點
則位勢(重節點數)的變化為l1+l2-h1-h2
平均攤還時間=代價+位勢變化=2(l1+l2)
現在只需證明l1+l2=O(logN)
而l1和l2是原右路徑上的輕節點數目,而輕節點左子樹重、右子樹輕,因此l1+l2至多為logN1+logN2,即O(logN)
而初始位勢為0,始終非負,命題得證。
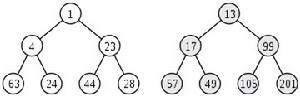
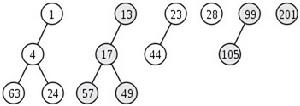
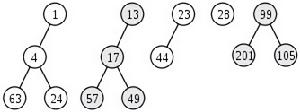
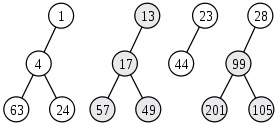
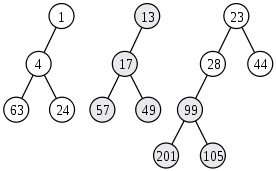
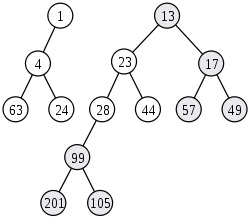
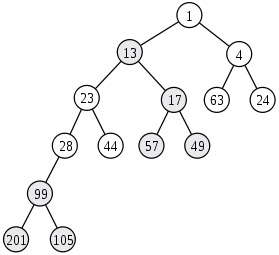
添加元素,就是合併原斜堆和一個節點的斜堆。
刪除刪除根節點,合併左右子樹。
