簡介
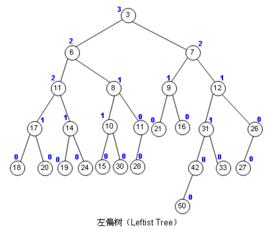
左偏樹(英語: leftist tree或 leftist heap),也可稱為左偏堆、左傾堆,是計算機科學中的一種樹,是一種優先佇列實現方式,屬於可並堆,在信息學中十分常見,在統計問題、最值問題、模擬問題和貪心問題等等類型的題目中,左偏樹都有著廣泛的套用。斜堆是比左偏樹更為一般的數據結構。
不同於斜堆合併的平均情況複雜度,左偏堆的合併操作的最壞情況複雜度為O(log n),而完全二叉堆為O(n),所以左偏堆適合基於合併操作的情形。
由於左偏堆已經不是完全二叉樹,因此不能用數組存儲表示,需要用連結結構。
定義
左偏樹是一種可並堆的實現。左偏樹是一棵二叉樹,它的節點除了和二叉樹的節點一樣具有左右子樹指針(left, right)外,還有兩個屬性: 鍵值和距離(英文文獻中稱為s-value)。鍵值用於比較節點的大小。距離的定義如下:
若且唯若節點 i 的左子樹且右子樹為空時,節點被稱作 外節點(實際上保存在二叉樹中的節點都是內節點,外節點是邏輯上存在而無需保存。把一顆二叉樹補上全部的外節點,則稱為extended binary tree)。節點i的 距離是節點 i 到它的後代中的最近的外節點所經過的邊數。特別的,如果節點 i 本身是外節點,則它的距離為0;而空節點的距離規定為 -1。
性質
節點的鍵值小於或等於它的左右子節點的鍵值。
節點的左子節點的距離不小於右子節點的距離。
節點的距離等於它的右子節點的距離加1。
一棵N個節點的左偏樹root節點的距離最多為log(N+1)-1。
1.節點的鍵值小於或等於它的左右子節點的鍵值。
2.節點的左子節點的距離不小於右子節點的距離。
3.節點的距離等於它的右子節點的距離加1。
4.一棵N個節點的左偏樹root節點的距離最多為log(N+1)-1。
操作
合併兩顆左偏樹
Java代碼實現合併兩棵左偏的最小樹:
root鍵值最小的樹的右子樹與其它樹合併;
上步合併結果作為與root鍵值最小樹的右子樹。
比較root的左右子樹的距離值(s-value),如果右子樹大於左子樹則交換兩棵子樹
1.root鍵值最小的樹的右子樹與其它樹合併;
2.上步合併結果作為與root鍵值最小樹的右子樹。
3.比較root的左右子樹的距離值(s-value),如果右子樹大於左子樹則交換兩棵子樹
其他操作
增加一個節點、刪除根節點、初始化一批數據,都是基於合併操作。