意義
它們是數學知識的具體表現,可以展現數學無窮魅力。
題型
口算題
例如:12+28=40,5×20=100,12 y+45 y=57 y,18 y÷12 y=1.5,18 x·18 y=324 xy等。目的是通過心算、口算、速算、巧算來 鍛鍊小學生的心智和快速反應能力。像在國小數學試中也有出現,初一數學試卷中也經常出現。
填空題
 數學題
數學題 數學題
數學題例如:已知 f( x )的定義域是[0,2],則 f( x -1)的定義域是[-,-1]∪[1,]。
判斷題
1、判斷題的作答方式:正確的答案在後面括弧里打''√ ",錯誤的答案在後面括弧里打“× ”,有時也用A,B選項.
2、判斷題的考點: 無外乎就是幾個知識點(更多的是概念的理解)容易混淆,考驗答題者對概念理解是否透徹。
3、做題技巧:審題清楚。
例如:平行的兩直線被第三條直線所截,內錯角相等。(√)
概述題
例如
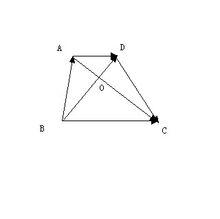
1.在梯形 ABCD中, AD// BC, AC⊥ BD,若 AD=2, BC=8, BD=6。
求:(I)對角線 AC的長;
 數學題
數學題(II)梯形的面積。
解: AC於 BD交接點為 O。
設 OC= x, OA= y, OD= z,則 BO=6- y,三角形而 AOD以 AD為底得高 h,三角形 BOC以BC為底的高h。因為 AC⊥ BD, AD=2, BC=8, BD=6,故△ AOD和△ BOC都為直接三角形。根據面積法得出兩個①等腰三角形 AOD(2 h= yz),②三角形 BOC(8 h=(6- z) x).③三角形 BDC(6 x=8( h+h))根據勾股定理求的2個等式,④ y + z =4,⑤ x +(6- z) =64,由①②③解得 x=4 y,通過這個 x, y的關係帶入④⑤可以解得 , , , , ,故梯形的高為 。則 AC=8. 梯形面積為 S=(2+8)×24÷5÷2=24。
2.在-44, -43, -42, …, 0, 1, 2, 3, …, 2005, 2006 這一串連續整數中,前100個數的和是多少?
方法一 解:前100個數的和=-(1+2+…+44)+(0+1+2+3+…+55)
=-(1+44)×44÷2+(1+55)×55÷2=550
方法二 解:前100個數的和=-(1+2+…+44)+(0+1+2+3+…+55)
= (-44+55)×100÷2=550
證明題
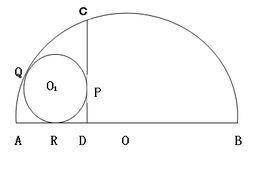
已知AB為半圓O的直徑,C為半圓上的一點,CD垂直AB,圓 O1切半圓於Q,切CD於P,切AB於R,求證:BC=BR。
選擇題
給出任意個選項,再把正確答案的序號填在括弧里,而不是正確答案,但自己首先要算出正確答案,再把正確選項的序號填在括弧里。(一般在答題卡是塗"A","B","C"或"D")
例如:
(1) 已知……,則x=(1) y=(2).
(2) A.1;2 B.2;1 C.0;0 D.無解
(3) 1=2+() a.1 b.2 c.3 d.4
計算題
要看清楚是不是直接寫得數,如果是,就不能寫過程,不是直接寫得數就要寫出過程,初學者過程要求詳細,學的時間久些就可以適當簡略些。記得要寫“ 解”(特別是解方程),在考試時這樣的題目因為解失分很不值,也要儘量不讓它失分。算完再驗算一下。直接將得數代入即可。
看圖題
沒有太多規律,可能是圖形、線段圖,也可能是統計圖,但是重點還是7個字: 審好題,反覆檢查。
套用題
在數學上,套用題分兩大類:一個是純數學套用。另一個是實際套用。
純數學套用就是指單獨的數量關係,構成的題目,沒有涉及到真正實際意義的量的存在及其關係。實際套用也就是有關於數學的生活題目。
套用題一般出現在國小的課本上,通常只涉及非負數的四則運算。在國中,一般都為列代數方程解套用題,或者是通過解直角三角形解決實際問題。在高中,往往有多種手段可供選擇,譬如函式、數列、不等式、導數、定積分、解斜三角形等。
筆者在套用題教學中採用以下分析方法,取得了較好的效果。
套用題主要是把正確的答案用不同的方法解決出來,並寫出解題過程,多做這樣的題目可以使人們的思維變得更好。 注意要寫答句和單位!
作用
對於學生
檢驗學生的數學學科掌握情況,對症下藥。
對於數學領域
可以演變成數學猜想、數學定理。
對於其他學科
可以將物理等理科的題目轉化為數學題,用數學方法解決。