數學微分法

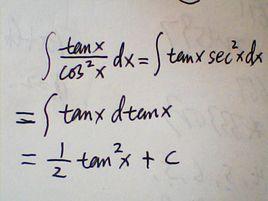
數學微分法是指根據邊際分析原理，運用數學上的微分方法，對具有曲線聯繫的極值問題進行求解，進而確定最優方案的一種決策方法。在用數學微分法進行決策時，凡以成本為判別標準時，一般都求極小值；凡以收入或利潤為判別標準時，一般都求極大值。這種方法廣泛運用於成本決策、存貨決策、定價決策之中。

程式

在財務決策中，存貨的經濟批量決策、最大利潤決策、最佳現金持有量決策、固定資產經濟使用年限等決策問題都要用到數學微分法。基本程式如下：  

(1)建立數學模型：y=f(x)，這裡的函式y既可以是利潤、資金、成本，也可以是生產批量或採購批量；

(2)對上述函式求導：y'=f'(x)，且令f'(x)=0，求x0 ；

(3)計算上述函式的二階導數，如果函式的二階導數小於零，則存在極大值；反之，存在極小值。在決策分析中，這一程式可以省略，因為根據實際情況可直接確定極大值還是極小值。