ρ擬對稱函式完全刻畫了上半平面的擬共形映射，容易看出，任何一個上半平面的擬共形映射在實軸上的限制滿足ρ擬對稱性。
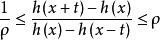擬對稱函式設h(x)是實軸上嚴格單調上升的連續函式，如果對一切x,t，t>0，對某一ρ成立，則稱h(x)為ρ擬對稱函式。
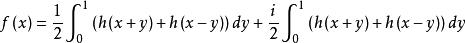擬對稱函式ρ擬對稱函式完全刻畫了上半平面的擬共形映射，容易看出，任何一個上半平面的擬共形映射在實軸上的限制滿足ρ擬對稱性；反之，博靈（Beurling,A.）與阿爾福斯（Ahlfors,L.V.）證明了任一實軸上的ρ擬對稱函式h(x)總可以擴張為上半平面的擬共形映射，他們通過h構造重要的擬共形映射（稱為博靈-阿爾福斯擴張），指出f是h的同胚擴張，而且是ρ 擬共形映射。
在空間中也有類似的擴張問題。
擬共形映射又稱 擬保角映射，原本是複分析中的一套技術手段，現已發展為一套獨立學科。其定義如下：
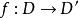擬對稱函式
擬對稱函式
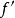擬對稱函式固定實數 K> 0。設 D, D' 為平面上的開子集，連續可微函式保持定向。若在每一點上其導數將圓映至離心率小於等於 K之橢圓，則稱為 K-擬共形映射，由此可見共形映射是 1-擬共形映射。
擬對稱函式 擬對稱函式若存在 K使為擬共形映射，則稱為 擬共形映射。
數學上，度量空間之間的擬對稱映射，是雙利普希茨映射的一個推廣。
介紹 定義 基本性質函式的定義：給定一個數集A，假設其中的元素為x。現對A中的元素x施加對應法則f，記作f（x），得到另一數集B。假設B中的元素為y。則y與x之間的等量關係...
詳細介紹 發展歷史 函式定義 表示方法 函式的特性的研究工作。內容簡介《實對稱矩陣的擬特徵值理論與套用》的中心內容是建立矩陣特徵值的一個新的套用分支——實對稱矩陣的擬特徵值（及向量）的分析方法。實對稱矩陣的擬特徵值的幾何意義在於它剛好與曲線的主法曲率成比例，因此具有...
函式（function），最早由中國清朝數學家李善蘭翻譯，出於其著作《代數學》。之所以這么翻譯，他給出的原因是“凡此變數中函彼變數者，則此為彼之函式”，...
“函式”由來 函式的特性 多項式函式 複變函數擬牛頓法(Quasi-Newton Methods)是求解非線性最佳化問題最有效的方法之一，於20世紀50年代由美國Argonne國家實驗室的物理學家W....
基本概念 基本思想 DFP方法 BFGS方法 對稱秩1（SR1）方法《多值邏輯函式結構理論研究》系統地闡述了多值邏輯函式的結構理論；詳細地介紹了部分多值邏輯中Sheffer函式的判定與構造問題。
圖書信息 內容簡介 目錄 前言《Copulas函式及其在水文中的套用》是2012年5月1日科學出版的圖書，作者是宋松柏、蔡煥傑、金菊良、康艷。宋松柏、蔡煥傑、金菊良、康艷吸編著的。
基本信息 編輯推薦語 內容提要 目錄§1.擬微分運算元的概念 §4.擬微分運算元代數 §2.擬微分運算元的微擬局部性
圖書信息 內容簡介 目錄《單葉函式與從屬原理》，是高建福編著，由中國科學技術大學出版社出版的書籍。
基本信息 內容簡介 前言