研究目的
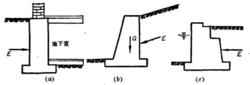圖1擋土牆是一種用以抵擋土體坍塌的結構物。它在土建工程中的套用較廣。如房屋建築中的地下室牆（圖1-a），道路工程中支持邊坡的牆（圖1-b），橋樑中的橋台（圖1-c）等。
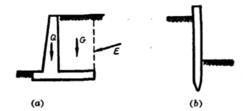圖2就擋土牆結構的特點可分為重力擋土牆（圖1）、薄壁擋土牆（圖2-a）和板樁擋土牆（圖2-b）三種。
重力擋土牆截面的高度和寬度是同量極的，牆依靠本身的自重Q來抵抗牆後的土壓力E，以維持平衡，這種擋土牆常用塊石或混凝土砌築而成。薄壁擋土牆普便是用鋼筋混凝土板建造的，牆的自重Q雖不大，但是因為有水平板上的土重G的幫助，也足以抵抗土壓力E。板樁擋土牆的截面高度較大而厚度很小，它是由木樁、鋼筋混凝土樁或鋼板樁所建造而成的，靠打入土內的深度來維持平衡。
作用於擋土牆上的土壓力E確定後，即可進行擋土牆的設計。在設計時首先要使擋土牆具有足夠的穩定性，以保證在土壓力作用下不會繞邊棱傾覆或沿牆底面滑動。
對擋土牆穩定性的研究，包括安全係數驗算和可靠度分析。
安全係數
擋土牆的安全係數驗算，通常包括抗傾覆穩定性和抗滑移穩定性驗算。
抗傾覆穩定性驗算
圖1（a）表示一具有傾斜基底的擋土牆，在牆重力和主動土壓力的作用下可能繞牆趾O點向外傾覆，抗傾覆力矩與傾覆力矩之比稱為抗傾覆安全係數K，應滿足下列要求：
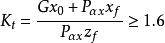擋土牆穩定性
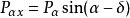擋土牆穩定性
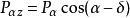擋土牆穩定性
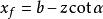擋土牆穩定性
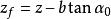擋土牆穩定性式中：
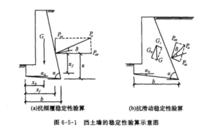圖1G——擋土牆每延米自重，kN/m；
x——擋土牆重心離牆趾的水平距離，m；
z——土壓力作用點離牆趾的高度，m；
b——基底的水平投影寬度，m；
P——主動土壓力在水平方向的分量，kN/m；
P——主動土壓力在垂直方向的分量，kN/m；
α——擋土牆牆背與水平面的夾角，度；
α——擋土牆基地的傾度，度；
δ——土對擋土牆牆背的摩擦角，由實驗確定，也可以按表1選用。
當地基軟弱時，在傾覆的同時，牆趾可能陷入土中，因而力矩中心O點向內移動，抗傾覆安全係數就將會降低，因此運用上式應注意地基土的壓縮性。
| 擋土牆情況 | 摩擦角δ |
| 牆背平滑，排水不良 | （0~0.33）φ |
| 牆背粗糙，排水良好 | （0.33~0.50）φ |
| 牆背很粗糙，排水良好 | （0.50~0.67）φ |
| 牆背與填土間不可能滑動 | （0.67~1.00）φ |
註：φ為牆背填土的內摩擦角標準值。
抗滑動穩定性驗算
在土壓力作用下，擋土牆有可能沿基礎底面發生滑動（圖1（b））。抗滑力與滑動力之比稱為抗滑安全係數K，應滿足下式要求：
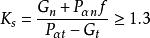擋土牆穩定性
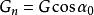擋土牆穩定性
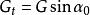擋土牆穩定性
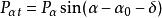擋土牆穩定性
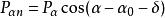擋土牆穩定性式中：
P——主動土壓力平行於基底面方向的分量，kN/m；
P——主動土壓力在垂直於基底面方向的分量，kN/m；
f——土對擋土牆基底的摩擦係數，由試驗確定，也可以按表2選用。
| 土的類別 | 摩擦係數 | |
| 粘性土 | 可塑 | 0.25~0.30 |
| 硬塑 | 0.30~0.35 | |
| 堅硬 | 0.35~0.45 | |
| 粉土 | 0.30~0.40 | |
| 中砂、粗砂、礫砂 | 0.40~0.50 | |
| 碎石土 | 0.40~0.60 | |
| 軟質岩石 | 0.40~0.60 | |
| 表面粗糙的硬質岩石 | 0.65~0.75 | |
註：1.對易風化的軟質岩和塑性指數I大於22的粘性土，基底摩擦係數應通過試驗確定；
2.對碎石土，可根據其密實程度、填充物狀況、風化程度等確定。
模糊可靠度
長期以來，擋土牆的設計均採用定值設計方法，以安全係數來表征擋土牆結構的穩定性程度。而事實上，在擋土牆穩定性分析中存在著大量的不確定性因素，主要包括隨機不確定性和模糊不確定性。所謂事件的隨機性，是指事件發生的條件不充分，使得在條件與事件之間不能出現必然的因果關係，從而事件的出現與否表現出不確定性。如土體的重度與內摩擦角等都可以看作是隨機變數，而擋土牆的失穩可以看作是隨機過程，可採用以可靠度理論為基礎的設計方法來研究。
“模糊”是人們表達含糊的概念、觀點和態度時使用的一個詞。所謂模糊性是指邊界不清楚，即在質上沒有確切的含義，在量上沒有明確的界限，是一種劃分上的不確定性。模糊性產生的根源在於客觀事物的差異存在著中間過渡，“亦此亦彼”的現象。例如，擋土牆的穩定性就是一個模糊概念，在失穩與穩定之間存在一個模糊過渡區。
可靠度分析
在結構可靠度分析與設計中，為了正確描述結構的工作狀態，必須明確規定結構安全、耐久、適用和結構失效的界限，這樣的界限稱為結構的極限狀態。結構的極限狀態實質上是結構工作狀態的一個閾值，若超過這一閾值，則結構處於不安全、不耐久或不適用的狀態；若沒有超過這一閾值，則結構處於安全、耐久、適用的狀態。如果用隨機向量表示結構的基本隨機變數X=(X1,X2,… ,Xn)，用g(°)表示描述結構工作狀態的函式，稱為結構功能函式，則結構的工作狀態可用下式表示：
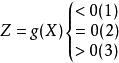擋土牆穩定性上式中：(1)失效狀態；(2)極限狀態；(3)可靠狀態。
如果用R表示結構的抗力，用S表示結構上的作用（荷載）效應。則結構的功能函式可表示為：
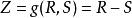擋土牆穩定性在擋土牆抗傾覆穩定性分析中，R為抗傾覆力矩，S為傾覆力矩。
在擋土牆抗滑穩定性分析中，R為抗滑力，S為滑動力。
在計算分析中，結構功能函式為非線性函式，若X1,X2,… ,Xn是結構中n個相互獨立的隨機變數，其平均值為μXi(i= 1,2,… n)，標準差為σXi(i= 1,2,… n)。將功能函式Z= g(X1,X2,… ,Xn)在隨機變數的平均值處展開為泰勒級數，即：
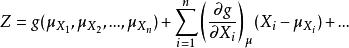擋土牆穩定性Z的平均值和方差可表示為：
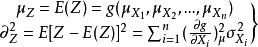擋土牆穩定性因此可靠度指標可表示為：
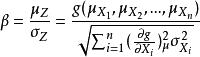擋土牆穩定性結構的失效機率可表示為：
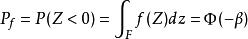擋土牆穩定性式中F表示結構的失效域，f(z)為結構功能函式的機率密度函式。
模糊可靠度計算
由於事物本身存在著中間過渡現象及對事物劃分標準邊界的不清晰，一個元素只是在一定程度上屬於一個集合，描述這種程度的就是模糊數學中的隸屬函式。當考慮擋土牆由“完全失穩”到“完全穩定”之間的中介過渡性時，引入可以表征擋土牆穩定性的隸屬函式μ(z)。
隸屬函式的形式通常可以採用模糊統計試驗的方法確定，或者從工程實際出發憑經驗選取某一理論隸屬函式，工程中常用的隸屬函式的形式有半梯形分布、半常態分配、嶺型分布等。
由於擋土牆的失穩既具有模糊性又具有隨機性，為一模糊隨機事件，根據模糊數學的理論，其發生的機率為：
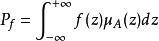擋土牆穩定性當μ表示失效程度時，μ接近於0時，失效的可能性小；當μ= 0.5時，處於最模糊狀態，可作為傳統分析時的極限平衡狀態；當μA= 1時，失效的可能性大。當μA(z)採用降半梯形分布時：
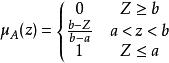擋土牆穩定性由於結構的功能函式具有隨機性，可用其均值進行模擬。
擋土牆失穩的模糊可靠度為：
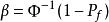擋土牆穩定性安全係數與可靠度關係
①重力式擋土牆滑移失穩的機理比較簡單，抗滑移原理明確，與重心位置無關，當截面積滿足抗滑要求且不改變基底尺寸的情況下，加大牆頂寬度有利於抗傾覆穩定性的要求。
②可靠度指標隨著對應安全係數的增大而增大，一直沿用的擋土牆驗算方法定性分析是正確的，但可靠度指標與安全係數的數值關係不明確。得出一種工況下的數值關係，具有一定的參考價值，但尚需進一步計算其他工況下的數值關係以便得出具有概括性的函式關係。
