描述複雜性理論
正文
用算法作工具來研究字元串所含的信息（即串的描述複雜度）的理論，又稱算法資訊理論。由於各種計算對象都可以用0，1組成的字元串(簡稱0，1串)來表示。任何計算過程（包括證明過程）都可轉化為對串的加工過程，在這個過程中串不斷地變換,所含信息也在變化,因此分析這種變化就能揭示計算和證明過程的某些內在屬性。在這種意義下可認為描述複雜性理論是把算法與信息結合起來的理論。描述複雜度 0，1串x所含信息可用對x的描述之長短來刻劃,可以認為串x的描述是構造x的指令組，串x的描述複雜度可直觀地定義為生成x的最短程式之長,記作K(x)。這個程式無輸入，其輸出為x。
作為普遍定義，K(x)必須客觀地反映x所含信息多少，不會由於採用不同計算模型下的程式概念而使對應的K(x)值截然不同。在可計算理論中已證明，現存的不同的計算模型A，B之間可以相互模擬,於是A模型下的程式PA結合模擬程式後，就成為B模型下的程式PB，因此在相差一個常數的意義下K(x)值是唯一確定的。
描述複雜性理論是在可計算性理論的發展和計算機廣泛套用的推動下發展起來的。60年代A.H.柯爾莫戈羅夫與柴廷各自獨立地提出描述複雜度概念，用以定義數的隨機性，並能較全面地提出關於程式長度的描述複雜性理論。
理論內容 描述複雜性理論的研究對象是0，1串以及它們變換時所含信息的變化。它可用於研究形式系統，分析公理所含信息與它推出的定理所含信息之間的關係，也可用於研究計算過程，從而得出計算所耗費資源的下界（見計算複雜性理論）和時間與空間的折換關係。
這個理論中大部分結果的證明是非構造性的，只從邏輯上推斷特定對象的存在性，並不具體構造出哪個對象。這種證明過程常遵循下述模式:對待證命題A採用反證法,利用逆命題“¬A成立”這事實來對已知複雜度為K的串x構作一個生成x的較短程式P,P之長小於K，從而得出矛盾的結果。
運用這種證法可得出K(x)的下述基本性質：
①作為x的函式K(x)是不可計算的。
②長為n的串中至少有一串,它們的描述複雜度是等於n的。顯然這樣的串是同長串中最複雜的,稱之為隨機串。
柴廷定理 柴廷1974年得出下列重要結果：對任何相容的公理化理論T,都存在一個常數CT＞0(它只依賴於T)，使K(x)＞CT這樣的命題在T內是不可證的。
若把T取作數論公理系統,在T內可表達K(x)＞CT這樣的命題,並且由K(x)的基本性質可知：對任何n都有長為n的串x使K(x)=n,因此當n充分大時,命題K(x)＞CT是成立的，但在T中卻不可證明。由此可推出,串的隨機性是不可證的。它改進了K.哥德爾關於數論公理統系不完全性定理,給出一個更具體的不可證命題：K(x)＞CT,從信息角度闡明了公理方法的局限性。
下界問題 運用相似的方法可對計算複雜性下界問題得出下列結果。
考慮語言L=｛x嶅x│x為0，1串，C為異於0，1的字元｝在多帶圖靈機（見多帶圖靈機模型）上的識別問題。用T(n)，S(n)分別表示時間、空間複雜度,其中n是輸入的長度。利用描述複雜性理論易於得到下述的時空折換關係：對任何一個識別L的多帶圖靈機，都存在常數C>0，當n充分大時，有T(n)S(n)＞Cn2。
可以證明，這樣的結果是不可改進的，即對通常的S(n)都可構造一台在C′n2/S(n)時間內識別L的機器。
多頭多維帶單元是圖靈機上線狀帶的推廣，它允許一條帶上有許多個讀寫頭,帶本身是多維的,它的基本命令允許帶頭沿任一方向移動一格,印出所注視符號等。這樣的存儲單元在功能上更接近實際存儲器。考慮帶頭多少對計算的影響時，得到的結果是：若d1≥2，d2＜d娝，h2＜h1，而一台h2頭d2維的具有跳頭功能的帶單元S能在T(n)時間內在線上模擬一台h1頭d1維單元的n條命令，則T(n)＞Cn
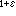，其中C與ε是正常數。 它從理論上說明增多帶頭會節省大量時間,反之,即使增強S其他方面的能力（如帶的維數加大到d娝-1,帶頭會一下子跳到另一帶頭處）也無法彌補由於減少帶頭而引起的惡果。
描述複雜性是研究某些性質不可證時的有力工具。通過發展、改進現有的方法，有希望對計算複雜性理論中某些重大問題提供一些方法，而且對某些具體問題的下界得出新的結果。
