簡介
在許多實際問題中，控制系統的狀態變數不是由直接測量得到的，而是通過某種觀測方法得到的，由某種觀測系統所得到的結果能否真實反映系統的狀態就是系統的可觀測性。
可觀測性是估計理論一個專業概念，反映狀態可估計性的能力。判定這種能力有兩種方法：一是將問題化歸為數學方程問題的求解。若數學上無解，表示此問題無解；若數學上有解，表示此問題能解；若數學上有一個解、兩個解、多個解、無窮多個解，則表示該問題的解的狀況。二是不將問題化為數學方程求解的形式，化為一個判定問題，只判定問題能解或不能解，這種判定形式是多種多樣的。
定義
可觀測性表示輸出可以完全反映系統狀態的特性，因此不僅要考慮系統的狀態方程還要考慮輸出方程。以考慮連續時間線性時變系統Σ為例，其狀態方程和輸出方程分別為：
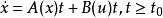控制系統可觀測性
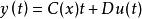控制系統可觀測性其中x為n維狀態，u為p維輸入，y為q維輸出，t為初始時刻。A為n×n維的系統矩陣，B為n×p維的輸入矩陣，C為q×n維的輸出矩陣，D為q×p維的傳輸矩陣，它們都是由系統結構和參數決定的。
對系統的運動進行分析可知，系統Σ狀態解的表達式為：
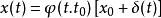控制系統可觀測性其中Φ(t，τ)為系統的狀態轉移矩陣，並且，如果表輸入材引起的等價狀態為ξ(t)
不難發現，在研究可觀測性，也就是狀態變數x(t)可由輸出變數y(t)反映的性質時，通常輸入以的等價狀態孝y(t)看作是初始狀態，從而可以把狀態方程中U的相關項去掉。由於只考慮狀態變數工(f)由輸出變數y(f)的反映性，所以在輸出方程中可去掉ξ(t)的相關項。
下面，基於系統的狀態空間描述Σ給出狀態和系統可觀測性的有關定義。
狀態的不可觀測性
指定一個時刻t∈J，如果存在一個時刻t∈J另t>t，使連續時間線性時變系統Σ以初始狀態為x(t)=x而的輸出y(t)恆為零，即對所有的t∈【t，t】，y(t)=0成立，則稱狀態x不可觀測的。
直觀上，輸出y(t)對以不可觀測狀態而為初始狀態導致的運動回響x(t)具有?‘過濾”作用，即x(t)不能被反映在y(t)中。可觀測性表征了輸出可以完全反映系統狀態運動的一種特定屬性。
系統的完全可觀測性
指定一個初始時刻t∈J，如果在時刻t∈J連續時間線性時變系統Σ狀態空間中所有不為零的狀態都不是不可觀測的，則稱系統在時刻t為完全可觀測的。
系統不完全可觀測的
指定一個初始時刻t∈J，如果在時刻t∈J連續時間線性時變系統Σ狀態空間中存在一個不為零狀態或者一個非空狀態集合是不可觀測的，稱系統Σ在時刻t∈J為不完全可觀測的。
從工程實際角度來看，系統為不完全可觀測是一種“奇異”狀況。一個實際的系統幾乎都能保證是可觀測的。這就是說，即使隨機地選取線性時不變系統係數矩陣A和C的元，那么幾乎也能保證使系統轉化為完全可觀測。
系統一致完全可觀測
如果在任意初始時刻t∈J，系統Σ均為完全可觀測，即系統的可觀測性無關於初始時刻t∈J的選取，則稱連續時間線性時變系統Σ為一致完全可觀測。
一致可觀測性屬於線性時變系統的特殊問題，對線性時不變系統來說，系統完全可觀測一定意味著一致完全能觀性。
研究意義
一個控制系統除具備調節與運算功能以外，還必須具備從生產過程獲得必要的信息和向生產過程發出控制命令的功能。現在擺在設計人員面前的一個問題，就是如何知道哪些信息是必要的，哪些信息是可要可不要的?也就是哪些狀態變數必須測量?這個問題正是可觀測性分析要作出的回答。
可觀測性分析有兩個方面的意義：
1.簡化檢測點，以達到節省側量儀表的目的。
2.目前尚有許多過程參數沒有檢測工具，在這種場合下，分析能否採用其他測量儀表代替，使許多無法檢測的參數，用間接測量的辦法，達到控制其狀態變化的目的。
可觀側性判斷準則
控制系統的可控性與可觀測性分析，是現代控制理論的一個重要內容。要分析一個系統的可觀測性，一般都要計算可觀測性判斷矩陣H。
通過對大量系統傳遞函式的分析，歸納六個重要準則：
1.沒有分支的最簡可測環節串接，由下游的狀態變數可以推斷上游的狀態變數。
2.一個支路下游的狀態變數，不能推斷另一個支路的狀態。
3.在同一支路里，不能由上游的狀態變數推斷下游的狀態變數。
4.由某一狀態能夠推斷前一個狀態的條件是：關聯的狀態變數必須線性無關。線性無關是表示一個狀態變數取定以後，可以由它唯一地決定另一個狀態變數。
5.觀測矩陣H的組成不應包含有與系統結構可以相約的因子。
準則5告訴我們：一個系統完全可觀測，至少必須能觀測最下游的狀態變數。假如需要引入其他狀態的觀測值，組成綜合觀測變數，必然使觀測矩陣包含有動態因子，在這種場合下，系統是否完全可控，應按準則5。
6.可觀測性分析與控制作用u所加入的位置無關。這個準則已為基本定理的推導所證明，因此，在分析系統可觀。測性的結構中，不應把控制作用當作支路看待。
