指數修勻法的含義
指數修勻法又叫指數平滑法(exponential smoothing,ES),由布朗(Robert G.Brown)所提出。布朗認為,時間序列的態勢具有穩定性或規則性,所以時間序列可被合理地順勢推延;他認為最近的過去態勢,在某種程度上會持續到未來,所以將較大的權數放在最近的資料。指數修勻法是預測中常用的一種方法,也用於中短期經濟發展趨勢預測,所有預測方法中,一次指數修勻法是用得最多的一種。簡單的全期平均法是對時間數列的過去數據一個不漏地全部加以同等利用;移動平均法則不考慮較遠期的數據,並在加權移動平均法中給予近期資料更大的權重;而指數修勻法則兼容了全期平均和移動平均所長,不捨棄過去的數據,但是僅給予逐漸減弱的影響程度,即隨著數據的遠離,賦予逐漸收斂為零的權數。也就是說指數修勻法是在移動平均法基礎上發展起來的一種時間序列分析預測法,它是通過計算指數平滑值,配合一定的時間序列預測模型對現象的未來進行預測。其原理是任一期的指數平滑值都是本期實際觀察值與前一期指數平滑值的加權平均。
計算公式
指數修勻法的計算公式為
 指數修勻法
指數修勻法 指數修勻法
指數修勻法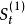 指數修勻法
指數修勻法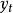 指數修勻法
指數修勻法式中, 為平滑係數; 為t時刻的一次指數平滑值; 為t時刻的實際值。
平滑係數的選擇
平滑係數選擇的原則
(1)如果時間序列波動不大,比較平穩,則平滑係數應取小一點,以減少修正幅度,使預測模型能包含較長時間序列的信息。
(2)如果時間序列具有迅速且明顯的變動傾向,則平滑係數應取大一點,以使預測模型靈敏度高些,以便迅速跟上數據的變化。
(3)在實用中,可多取幾個值進行試算,取使預測誤差較小的平滑係數。
初始值的確定
 指數修勻法
指數修勻法初始值 的確定
(1)當時間序列的數據<20個時,可選用第一期數據為初始值。
(2)當時間序列的數據>20個時,可取最初幾期的實際值的平均值作為初始值。
例題解析
某地某類房地產2008-2012年價格資料如表1所示,試用指數修勻法求該房地產2013年的價格。
| 年份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 價格 | 2000 | 2400 | 2380 | 2500 | 2600 | |
| 預測值 | 2000 | 2160 | 2248 | 2348.8 | 2449.3 |
 指數修勻法
指數修勻法解:取 ,則
2009年平滑值=0.4 X2000+(1-0.4)×2000=2000(元/m)
2010年平滑值=0.4×2400+(1-0.4)×2000=2160(元/m)
2011年平滑值=0.4×2380+(1-0.4)×2160=2248(元/m)
2012年平滑值=0.4×2500+(1-0.4)×2248=2348.8(元/m)
2013年平滑值=0.4×2600+(1-0.4)×2348.8=2449.3(元/m)
則2013年該房地產評估價格為:2449.3(元/m)。

