基本介紹
指數里含有未知數的不等式叫作 指數不等式。
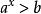 指數不等式
指數不等式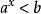 指數不等式
指數不等式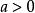 指數不等式
指數不等式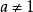 指數不等式
指數不等式形如 或 ( ,且 )的不等式叫作基本指數不等式或最簡指數不等式。下列形式的每個不等式叫做初等指數不等式 :
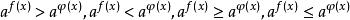 指數不等式
指數不等式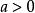 指數不等式
指數不等式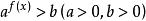 指數不等式
指數不等式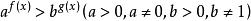 指數不等式
指數不等式其中 。還有形如,等的不等式也都是指數不等式。
指數不等式的解法
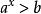 指數不等式
指數不等式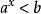 指數不等式
指數不等式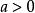 指數不等式
指數不等式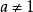 指數不等式
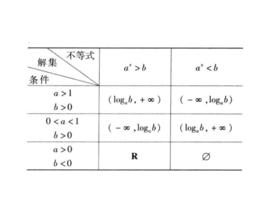
指數不等式①形如 或 ( ,且 )的不等式的解法
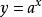 指數不等式
指數不等式理論依據是指數函式 的單調性。
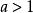 指數不等式
指數不等式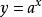 指數不等式
指數不等式(1)當 時,函式 是增函式;
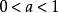 指數不等式
指數不等式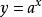 指數不等式
指數不等式(2)當 時,函式 是減函式。
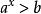 指數不等式
指數不等式下面我們研究不等式 的解法:
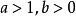 指數不等式
指數不等式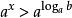 指數不等式
指數不等式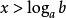 指數不等式
指數不等式(1)當 時,原不等式即為 ,所以 ;
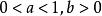 指數不等式
指數不等式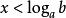 指數不等式
指數不等式(2)當 時,則有 ;
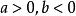 指數不等式
指數不等式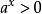 指數不等式
指數不等式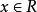 指數不等式
指數不等式(3)當 時,因 ,故 。
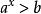 指數不等式 指數不等式 | 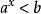 指數不等式 指數不等式 | |
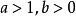 指數不等式 指數不等式 | 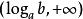 指數不等式 指數不等式 | 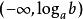 指數不等式 指數不等式 |
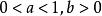 指數不等式 指數不等式 | 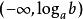 指數不等式 指數不等式 | 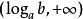 指數不等式 指數不等式 |
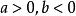 指數不等式 指數不等式 | 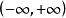 指數不等式 指數不等式 |  指數不等式 指數不等式 |
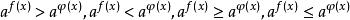 指數不等式
指數不等式②形如的解法
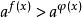 指數不等式
指數不等式不等式::
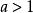 指數不等式
指數不等式當 時等價於不等式
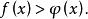 指數不等式
指數不等式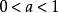 指數不等式
指數不等式當時等價於不等式
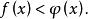 指數不等式
指數不等式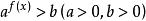 指數不等式
指數不等式③ 形如的解法
兩邊取常用對數:
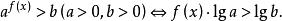 指數不等式
指數不等式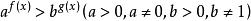 指數不等式
指數不等式④形如
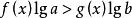 指數不等式
指數不等式兩邊取常用對數:。