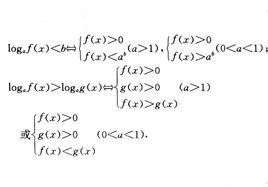基本概念
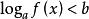簡單對數不等式
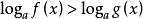簡單對數不等式形如(a>0,且a≠1)和，(a>0，且a≠1)的不等式叫做最簡對數不等式 。
解最簡對數不等式可根據對數函式定義，對數函式的定義域及其單調性轉化為代數不等式組然後進行求解。
對數不等式的解法
解對數不等式的一般方法.即求式中未知數的所有滿足該式的數值的方法.對於能用初等方法求解的一些簡單對數不等式，主要有如下解法 ：
1同底法。形如
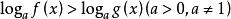簡單對數不等式的不等式。
當0<a<1時，可以轉化為解不等式組
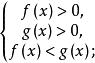簡單對數不等式當a>1時，可轉化為解不等式組
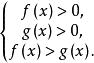簡單對數不等式若在給定的不等式中，各個對數的底數不同，例如logf(x)>logg(x)(a>0，a≠1，b>0，b≠1)，應先換成同底對數，使不等式變成
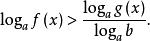簡單對數不等式當a>1且b>1或a>1且0<b<1時，它相應轉化為不等式組
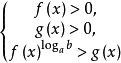簡單對數不等式或
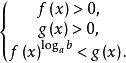簡單對數不等式注意0<a<1時，函式logx單調下降；故當0<a<1且b>1或0<a<1且0<b<1時，它分別轉化為解不等式組
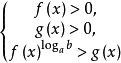簡單對數不等式或
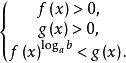簡單對數不等式2.換元法。解形如
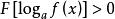簡單對數不等式或
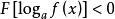簡單對數不等式的不等式：令y=logf(x)，原不等式可轉化為解不等式F(y)>0(或F(y)<0)，再轉化為解最簡對數不等式或不等式組，即得原不等式的解 。
3.指數式法。形如logf(x)>b(b>0)的不等式，當0<a<1時，可化為f(x)<a ，當a>1時，可轉化為f(x)>a ，可求它們在條件f(x)>0下的解;形如logf(x)<b的不等式，可解不等式組
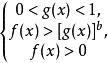簡單對數不等式與
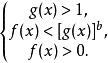簡單對數不等式它們的解集的並集就是原不等式的解集 。
