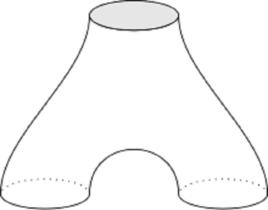
綜述
在 拓撲量子場論中 ，相關函式並不取決於時空的度量。這意味著理論對時空形狀的改變不敏感：時空彎曲或收縮時，相關函式並不因此改變。因此，它們是拓撲不變數。
在粒子物理學中常用的、平坦的閔可夫斯基時空中，拓撲場論並不十分有趣。這是由於閔可夫斯基空間可以被收縮成一點，所以其中的TQFT只計算出平凡的拓撲不變數。因此，TQFT通常在黎曼曲面等彎曲的時空上研究。大多數已知的拓撲場論定義在5維的彎曲時空中。更高維度的拓撲場論似乎存在，但人們未能清楚理解這些理論。
量子引力被相信是背景獨立的（在某種意義上），而TQFT恰好能提供背景獨立的量子場論的例子。這一特性促進了現行的對此類模型的理論探索。
20世紀70年代，阿爾伯特·施瓦茨就研究過一種拓撲量子場論（阿貝爾的陳-塞蒙斯場論）。80年代末，在麥可·阿蒂亞啟發下，研究了三個拓撲量子場論：一個由超對稱楊-米爾斯場論扭變得到，用以將唐納森不變數和弗勒爾瞬子同調解釋為量子物理對象；第二個是非阿貝爾的陳-塞蒙斯場論，用以將瓊斯多項式及其衍生物解釋為量子物理對象；第三個由超對稱Σ模型扭變得到，用以將格羅莫夫的贗全純曲線和弗勒爾的拉格朗日同調解釋為量子物理對象。1994年威滕套用弦論學家得到的強弱對偶結果將唐納森不變數等價為更易計算的塞伯格-威滕不變數。進入21世紀，威滕等人又研究了具有更多超對稱的楊-米爾斯場論的扭變，並將數學中的幾何郎蘭茲對偶解釋為量子場論中的強弱對偶。威滕等人進一步發現，Σ模型、陳-塞蒙斯場論、以及超對稱楊-米爾斯場論之間有千絲萬縷的聯繫，它們都可以包含在弦論或者M-理論中，在這個大框架之下，瓊斯多項式的範疇化——霍萬諾夫同調被解釋為量子物理對象。
在凝聚體物理學中，拓撲量子場論是拓撲有序態的低能有效理論，例如分數量子霍爾態、弦網凝聚態及其他強關聯液態自旋量子。
具體模型
已知的 拓撲場論可分為兩個大類：施瓦茨類TQFT與威滕類TQFT。後者有時被稱為上同調場論。
施瓦茨類TQFT
在施瓦茨類TQFT中，系統的相關函式或配分函式可由度量獨立的作用量泛函的路徑積分計算出來。例如，在BF模型中，時空為二維流形 M，可觀察量由2-形式 F、輔助標量 B以及它們的導數所構造得到。作用量（決定了路徑積分）為
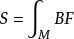拓撲量子場論時空度量在理論任何地方都沒有出現，因此這個理論顯然是拓撲不變的。第一個TQFT的例子於1977年由A. Schwarz給出，它的作用量泛函是
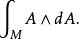拓撲量子場論另一個較為著名的例子是陳–西蒙斯理論，可用於計算紐結不變數。一般而言配分函式取決於度量，但以上兩例得證為度量獨立。
威滕類TQFT
第一個威滕類TQFT的例子出現於威滕1988年的論文（Witten 1988a）中，即4維的拓撲楊–米爾斯理論。雖然其中的作用量泛函包含時空度量 g，但是在拓撲扭曲之後，理論變為度量獨立。而系統應力-能量張量 T對度量的獨立性則取決於BRST-運算元是否閉合。遵循著威滕的例子，人們在拓撲弦論中找到了大量其它的例子。
後續發展
拓撲量子場論對塞伯格—威滕規範場論、拓撲弦理論、紐結理論和量子理論的關聯、和量子紐結不變數等有諸多套用。此外，它為數學和物理都提供了非常有趣的研究對象。最近，TQFT中的非局部運算元成為重要的研究方向。如果弦理論被視作根本理論，那么非局部TQFT則是為局部弦理論提供一個簡化計算的逼近的非物理的模型。
