詞條概述
拓撲量子計算是近十幾年發展起來的一門新穎的交叉學科,涉及到量子計算,拓撲學,拓撲量子場論,以及含拓撲序的凝聚態物理等。拓撲量子計算利用多體系統中的拓撲量子態來存儲和操控量子信息,具有內在的容錯能力,給量子計算的物理實現帶來了希望,也促進了我們對物質拓撲量子行為的探索。
出現背景
量子計算機由於其超越經典計算機極限的強大並行運算能力,成為二十一世紀量子物理學家們夢寐以求的目標。
然而,學術界公認的長期困擾其物理實現的最大問題“消相干效應”——由於量子計算機不可避免地與環境耦合而產生的各種噪聲從而使計算過程產生各種錯誤——一直沒有得到很好的解決。國際上以往提出的眾多量子糾錯方案中,一般採用對每一步邏輯操作都進行量子糾錯的方法。這樣,為了可擴展量子計算能夠有效進行,要求每一步邏輯操作的錯誤發生率都不得高於10量級,而這么低的容錯率是目前任何實驗手段都無法實現的。
理論依據
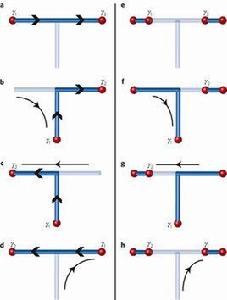
在含拓撲序的二維強關聯繫統中,可能存在一類稱為任意子的奇異粒子。與三維空間中的玻色子和費米子不同,任意子遵循阿貝爾統計或非阿貝爾統計。非阿貝爾任意子可以用來編碼量子比特,拓撲地存儲量子信息。非阿貝爾任意子在2+1維時空中的世界線形成辮子。我們可以利用這些辮子來構造普適的拓撲量子計算門,從而進行任意的拓撲量子操作。由於辮子拓撲的離散性,拓撲量子計算具有內在的容錯能力,局域的微擾不影響拓撲量子信息的存儲與處理。然而在龐大的辮子空間中有效地構造普適的拓撲量子計算門並非易事。通過把雙量子比特門分解為單量子比特門,普適的拓撲量子計算門的有效構造成為可能。辮子拓撲的離散性啟發我們對冗餘自由度引入幾何誤差,從而得到低泄漏的雙量子比特門。進而我們分解單量子比特門,結合引入誤差減小誤差的思想,我們得到了高精度單量子比特門。同時我們對拓撲量子計算算法中的自由度也作了探索。我們還構造了類重整化群的量子編譯算法,從而在理論上達到了任意精度的拓撲量子計算。
研究現狀
 拓撲量子計算
拓撲量子計算近年來,學術界提出了拓撲量子糾錯這一全新概念,把量子態的拓撲性質套用於量子糾錯過程中,從而將量子糾錯中可容忍的最高邏輯操作錯誤發生率提高了三個數量級,達到10量級。拓撲量子糾錯方案大大降低了對操作精度的要求,達到了現有實驗技術可以實現的水平,是目前已知擁有最高容錯率的量子計算方案,從而使得可擴展容錯性量子計算在現實條件下成為可能。
 拓撲量子計算
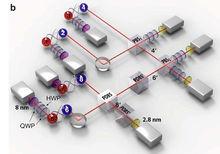
拓撲量子計算在中科院、科技部和國家自然科學基金委的支持下,潘建偉研究小組經過三年的艱苦努力,創造性地發展了一套全新的實驗技術,將雙光子糾纏的亮度提高了4倍,從而使得製備八光子簇態的總效率至少提高了200倍,僅用八十天時間就完成了實驗,這在以前幾乎是不可能實現的。同時,研究人員還設計了一種特殊的、濾除噪聲的八光子干涉儀,成功製造出並觀測到了具有拓撲性質的八光子簇態,並以此簇態為量子計算的核心資源,實現了拓撲量子糾錯。
實驗結果顯示,在拓撲量子計算的過程中可以完全糾正出現在任意量子比特上的單比特錯誤,而且當每個量子比特都以相同機率發生錯誤時,受保護的量子關聯的有效錯誤率會大大降低。這項工作在實驗上邁出了可擴展容錯性量子計算的第一步,在量子計算領域具有里程碑式的意義,它將有力地推動可擴展量子計算的發展,為將來成功實現真正的量子計算打下堅實的基礎。