性質
1.物理上提出的“拋體運動”是一種理想化的模型，即把物體看成質點，拋出後只考慮重力作用，忽略空氣阻力。
2.物體在做拋體運動時，只受到重力作用。
3.拋體運動加速度恆為重力加速度g，加速度恆定，則在相等的時間內速度變化的量相等，即△v=g△t。並且速度變化的方向始終是豎直向下的，拋體運動一定是勻變速運動，如果初速度的方向和重力方向在同一條直線上，物體將做勻變速直線運動，加速度大小為g；如果速度的方向和重力的方向不在同一條直線上，物體將做勻變速曲線運動，物體加速度的大小也為g，因為只受重力，加速度大小恆定為g，且方向豎直向下。
研究方法
研究方法：用運動的合成與分解方法研究平拋運動。
水平方向：勻速直線運動。
豎直方向：自由落體運動。
分解方法
一般的處理方法是將其分解為兩個簡單的直線運動。
1.最常用的分解方法是：平拋運動水平方向上是勻速直線運動，豎直方向上是自由落體運動；斜拋運動水平方向上是勻速直線運動，豎直方向上是豎直上拋運動。
2.在任意方向上分解：有正交分解和非正交分解兩種情況，無論怎樣分解，都必須把運動的獨立性和獨立作用原理結合進行系統分解，即將初速度、受力情況、加速度及位移等進行相應分解 。
運動公式
平拋運動
1.水平方向初速度：v
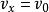拋體運動2.水平方向速度：
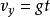拋體運動3.豎直方向速度：
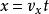拋體運動4.水平方向位移：
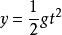拋體運動5.豎直方向位移：
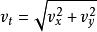拋體運動6.合速度：
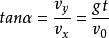拋體運動7.合速度方向與水平夾角α滿足：
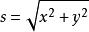拋體運動8.合位移：
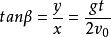拋體運動9.位移方向與水平夾角β滿足：
斜拋運動
1.水平方向初速度：v（初始方向為正）
2.豎直方向初速度：v（豎直向上為正）
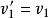拋體運動3.水平方向速度：
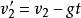拋體運動4.豎直方向速度：
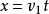拋體運動5.水平方向位移：
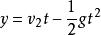拋體運動6.豎直方向位移：
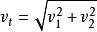拋體運動7.合速度：
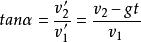拋體運動8.合速度方向與水平夾角α滿足：
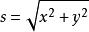拋體運動9.合位移：
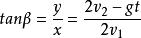拋體運動10.位移方向與水平夾角β滿足：
拋體運動的對比
| 概 念 | 性質 | 運動分解 | 速度 (以Vo方向為正方向) | 位移 | 軌跡方程式 |
| 豎直上 拋運動 | 加速度為重 力加速度g 的勻變速直 線運動 | 豎直方向： 勻速直線運 動和自由落 體運動 | V=Vo-gt | S=Vot-½gt² | |
| 斜上拋 運動 | 加速度為重 力加速度g 的勻變速曲 線運動 | 豎直方向： 豎直上拋 運動水平 方向：勻 速直線運 動 | V 水平=vo×cosθ V豎直=V0×sinθ-gt | S 水平=Vo×t×cosθ S 豎直=Vo×t×sinθ-(gt²)/2 | y=xtanθ-(gx²)/2(v0cosθ)² |
| 平拋運 動 | 加速度為重 力加速度g 的勻變速 曲線運動 | 豎直方向： 自由落體 運動水平 方向：勻 速直線運 動 | V =√{Vo²+(gt)²} | S=√{(Vot)²+(½gt²)²} | y=gx²/2vo² |
| 斜下拋 運動 | 加速度為重 力加速度g 的勻變速曲 線運動 | 豎直方向： 豎直下拋 運動水平 方向：勻 速直線運 動 | V 水平=V0×cosθ V豎直=V0×sinθ+gt | S 水平=v0×t×cosθ S 豎直=v0×t×sinθ+(gt²)/2 | y=xtanθ+gx²/2(v0cosθ)² |
| 豎直下 拋運動 | 加速度為 重力加速 度g的勻加 速直線運動 | 豎直方向： 勻加速直 線運動和 自由落體 運動 | V=Vo+gt | S=Vot+½gt² |
