人物生平
早年生活
拉馬努金出生於印度東南部泰米爾納德邦的埃羅德。1898年，在他十歲的時候，進入貢伯戈訥姆一所中學，在那裡他似乎第一次接觸到正規的數學。11歲時，他已經掌握了住在他家的房客的數學知識，他們是政府大學的學生。13歲時，他就掌握了借來的高等三角學的書里的知識。他的傳記作家稱他的天才在14歲時開始顯露。他不僅在他的學生歲月里不斷獲得榮譽證書和獎學金，他還幫學校處理把1200個學生（各有不同需要）分配給35個教師的後勤事務，他甚至在一半的給定時間內完成測驗，這已經顯示出他對無窮級數的熟練掌握；他那時的同校的人後來回憶說：“我們，包括老師，很少能理解他，並對他‘敬而遠之’”。但是，拉馬努金在其他科目無法集中注意力，並在高中考試中不合格。在他生活的這個時段，他也相當窮困，經常到了挨餓的地步。
成年工作
在印度的成年階段因為結了婚，他必須找到工作。帶著他的數學計算能力，他在真奈（舊稱馬德拉斯）到處找抄寫員的工作。最後他找到了一個工作，並在一個英國人的建議下和劍橋的研究人員聯繫。
作為真奈總會計師事務所的職員，拉馬努金奢望可以完全投入到數學中而不用做其他工作。他懇請有影響的印度人給予支持，並在印度數學期刊上發表了一些論文，但並未成功找到經濟支持。到這個時候，慕克吉（AshutoshMukherjee）爵士試圖支持他的事業。
展示才能
在1913年拉馬努金髮了一長串複雜的定理給三個劍橋的學術界人士貝克（H.F.Baker）、霍布森（E.W.Hobson）、哈代（G.H.Hardy），只有三一學院的院士哈代注意到了拉馬努金定理中所展示的天才。
讀著不知名和未經訓練的印度數學家的突然來信，哈代和他的同事利特爾伍德（J.E.Littlewood）評論道：“沒有一個定理可以放到世界上最高等的數學測試中。”雖然哈代是當時著名的數學家而且是拉馬努金所寫的其中幾個領域中的專家，他還是說很多定理：“完全打敗了我”、“我從沒見過任何像這樣的東西。”
作為他的成果的一個例子，拉馬努金給出了漂亮的連分數：其中是黃金分割。
晚年趣聞
拉馬努金病重，哈代前往探望。哈代說：“我乘計程車來，車牌號碼是1729，這數真沒趣，希望不是不祥之兆。”拉馬努金答道：“不，那是個有趣得很的數。可以用兩個立方之和來表達而且有兩種表達方式的數之中，1729是最小的。”（即1729 = 1³+12³= 9³+10³，後來這類數稱為的士數。）
利特爾伍德回應這宗軼聞說：“每個整數都是拉馬努金的朋友。”
人物成就
包括拉馬努金自己的發現和那些在和哈代的合作中發展和證明的定理，有高度合成數的性質 ，整數分割函式和它的漸近線、拉馬努金θ函式 。
他也在下列領域做出重大突破和發現： 伽馬函式 、模形式 、發散級數 、超幾何級數 、質數理論 。
雖然很多命題都可以稱為拉馬努金猜想，有一個特別適合這個稱號，它在後續工作中非常有影響。拉馬努金猜想是一個斷言，這是關於τ-函式的係數大小的，而那是一個模形式理論中的典型尖形式（cuspform）。這在幾十年後被證明為魏爾猜想的證明的一個結果，歸約步驟是很複雜的。
人物評價
拉馬努金是印度在過去一千年中所誕生的超級偉大的數學家。他的直覺的跳躍甚至令今天的數學家感到迷惑，在他死後70多年，他的論文中埋藏的秘密依然在不斷地被挖掘出來。他發現的定理被套用到他活著的時候很難想像到的領域。（引自卡尼蓋爾所著傳記《知無涯者：拉馬努金傳》第3頁）
美國作家羅伯特·卡尼蓋爾所著傳記《知無涯者：拉馬努金傳》被中國數學家，武漢大學前校長齊民友先生等翻譯成中文。
人物經歷
天才與貧困
1887年12月22日，拉馬努金出生於印度泰米爾納德邦埃羅德縣的一個沒落的婆羅門家庭。父親是一家布店的小職員，每月只有20盧比的工資，一家7口人就靠這點微薄的收入維持生活。小時候他大部分的時間是在祖母家裡度過的。從小他就喜歡思考問題，曾問老師在天空閃耀的星座的距離，以及地球赤道的長度。在12歲時開始對數學發生興趣，曾問高班同學：“什麼是數學的最高真理？”當時同學告訴他“畢達哥拉斯定理”（即中國人稱“勾股定理”）可以作為代表，這引起了他對幾何學的興趣。差不多在這個時候，他對等差級數和等比級數的性質自己做了研究。他那時的同學後來回憶說：“我們，包括老師，很少可以理解他，並對他‘敬而遠之’”。
他15歲時，朋友借給他英國數學家卡爾（G. Carr）寫的《純粹數學與套用數學概要》一書。該書收錄了代數、微積分、三角學和解析幾何的五千多個方程，但書中沒有給出詳細的證明。這正好符合拉馬努金的胃口，他把每一個方程式當成一個研究題，嘗試對其進行獨特的證明而且還對其中一些進行推廣。這花去了他大約5年的時間，留下了幾百頁的數學筆記。他證明了其中的一些方程，而以後他研究的基礎卻受益於這本書。
拉馬努金在貢伯戈納姆讀高中，畢業時各項成績突出，被校長形容為“用滿分也不足以說明他如此出色”。但進入當地著名的貢伯戈納姆學院後，他把全部精力投入數學研究，導致其他科目不及格；他不僅失去了獎學金，而且被學校開除。1905年，18歲的他為此離家出走3個月。一年後，拉馬努金被馬德拉斯的帕凱亞帕學院錄取，但這個數學成績優異的學生，還是難以逃脫被開除的命運，他的5門文科課程兩次不及格。此後拉馬努金開始做家教維持生計，同時從圖書館借來數學書，然後把自己的研究結論寫在筆記本里。
根據印度的習俗，他家人在1909年為他安排了婚事，妻子是一個9歲的女孩，在當時的印度這是相當常見的。有了家而且是長子，必須幫助家裡解決一些生活費用，他不得不極力尋找工作，後來朋友艾亞爾（S. Aiyar）推薦他去找馬德拉斯港務信託處官員拉奧（R. Rao）。拉奧是一個有錢的人，也是一個數學愛好者，他很賞識拉馬努金的數學才能。他認為拉馬努金只適合搞數學而不適合做其他工作，因此寧願每個月給他一些錢，讓他掛名不上班，在家專心從事數學研究。
拉馬努金只好接受這些錢，又繼續他的研究工作。每天傍晚時分才在馬德拉斯的海邊散步和朋友聊天作為休息。有一天一個老朋友遇到他，就對他說：“人們稱讚你有數學的天才！”拉馬努金聽了笑道：“天才？你看看我的臂肘吧！”他的臂肘的皮膚顯得又黑又厚。他解釋他日夜在石板上計算，用破布來擦掉石板上的字太花時間了，他每幾分鐘就用肘直接擦石板的字。朋友問他既然要作這么多計算為什麼不用紙來寫。拉馬努金說他連吃飯都成問題，哪裡有錢去買紙來算題呢！原來拉馬努金覺得依靠別人生活心裡很是慚愧，已經有一個月不去拿錢了。
1911年，拉馬努金的第一篇論文“關於伯努利數的一些性質”發表在《印度數學會會刊》上，從此他開始了與數學界同行的正式交流。拉馬努金在他的第二篇論文裡發表了一系列共14條關於圓周率π的計算公式；神奇的是，其中一條公式每計算一項就可以得到8位的十進制精度。
巧遇伯樂
由於印度當時的數學水平不高，國內幾乎沒有人能看懂拉馬努金的研究成果。於是，艾亞爾極力主張他把研究成果寄給英國數學家，最初的兩個數學家都未回音。1913年1月16日，他再次鼓起勇氣寫信給第三個數學家——劍橋大學教授哈代（G. Hardy）；信是這樣開頭的，“尊敬的先生，謹自我介紹如下：我是馬德拉斯港務信託處的一個職員……我未能按常規念完大學的正規課程，但我在開闢自己的路……本地的數學家說我的結果是‘驚人的’……如果您認為這些內容是有價值的話，請您發表它們……”他還給哈代寄去了一大堆自己研究得出的數學公式和命題；由於沒有證明的過程，有些連哈代也不大明白。哈代在諮詢了另一個英國數學家、他的合作夥伴李特爾伍德（J. Littlewood）之後，認定拉馬努金是一個難得的數學天才。拉馬努金多少有些運氣，哈代的慧眼識金，使得拉馬努金能夠在1914年進入劍橋大學。這則動人故事如今已成為數學史乃至科學史上的傳奇故事之一，同時作為兩個人學術生涯的轉折點——拉馬努金因哈代而嶄露頭角，哈代因拉馬努金而增光溢彩。
按哈代的說法，拉馬努金總是和藹可親，性情很好。但可以肯定，拉馬努金初到劍橋對哈代超出數學範圍的談話幾乎不懂。他聽哈代說話時似乎總帶著耐心的微笑，面容友善、真誠，但即使是談論數學，由於他們受教育程度不同，用詞及表述也就有差異。拉馬努金是自學的，他對現代學術意義上的嚴謹一無所知，在某種程度上他不知道什麼叫證明，於是哈代就向他演示如何寫出嚴謹的數學證明。有一次哈代喝醉酒以後曾經寫道，如果拉馬努金能受到更好的教育，將少一點拉馬努金的特性。當他清醒以後，他說那些話是胡說，應該說如果拉馬努金受到了更好的教育，他將會比現在更出色。
拉馬努金是個有神論者，哈代則是個無神論者，但他們卻能為數學而進行合作研究；在5年裡，他們共同發表了28篇重要論文。哈代曾將這段經歷描述為“我一生中最浪漫的事件”。因為在數學上的卓越成就，拉馬努金31歲就當選為英國皇家學會的外籍會員（亞洲第一人）以及劍橋大學三一學院的院士（印度第一人），走到了他的榮譽最高峰。
由於拉馬努金是個虔誠的婆羅門教徒，絕對奉行素食主義，在英國生活那段時間，他自己煮食物，常常因研究而忘記吃飯，加上冬天寒冷的天氣，他的身體越來越衰弱，1917年常感到身上有無名的疼痛。後來才發現他患上了當時難以醫治的肺結核病。有一天哈代去醫院看他時，抱怨所乘的計程車牌號1729是個不吉利的數字；而拉馬努金的第一反應則是，這是個有趣的數字，因為這個整數可以寫成12的立方與1的立方之和，也可以寫成10的立方與9的立方之和。後來李特爾伍德回應這宗軼聞說：“每個整數都是拉馬努金的朋友。”
拉馬努金思鄉心切，卻因為一戰爆發而無法回國。這一度令他變得抑鬱，甚至試圖臥軌自殺。1919年4月，他終於回到印度，但回家之後的生活並不愉快，且病情日漸加重。1920年4月26日，他病逝於馬德拉斯，年僅32歲。他身後留下了一份使人著魔的、深奧的數學遺產，其中包含了大量沒有證明的公式和命題。許多數學家都致力於這方面的研究，一直到1997年，才總算是完成了其中的一部分，並整理成5大卷出版。
神秘的直覺
拉馬努金的數學貢獻為現代數學家從事數學研究提供了很好的史料，對現代數學的發展也產生了難以估量的影響。他在堆壘數論特別是整數分拆方面做出了重要貢獻，在橢圓函式、超幾何函式、發散級數等領域也有不少成果。他有著很強的直覺洞察力（可稱之為“數感”），雖未受過嚴格數學訓練，卻能獨立發現了近3900個數學公式和命題。他經常宣稱在夢中娜瑪卡爾女神給其啟示，早晨醒來就能寫下不少數學公式和命題。他所預見的數學命題，日後有許多得到了證實。如比利時數學家德利涅（V. Deligne）於1973年證明了拉馬努金1916年提出的一個猜想，並因此獲得了1978年的菲爾茲獎。
除了在純粹數學方面做出卓越的成就以外，拉馬努金的理論還得到了廣泛的套用。他發現的好幾個定理在包括粒子物理、統計力學、計算機科學、密碼技術和空間技術等不同領域起著相當重要的作用，甚至晶體和塑膠的研製也受到他創立的整數分拆理論的啟發，而他在黎曼ζ函式方面的研究成果，現在已經與齒輪技術的進步掛上了鉤，還被用於測溫學及冶金高爐的最佳化。他生命中的最後一項成果——模仿θ函式有力地推動了用孤立波理論來研究癌細胞的惡化和擴散以及海嘯的運動；最近有專家認為，這一函式很可能被用來解釋宇宙黑洞的部分奧秘，而令人吃驚的是，當拉馬努金首次提出這種函式的時候，人們還不知道黑洞是什麼。
拉馬努金的亦師亦友哈代曾感慨道：“我們學習數學，拉馬努金則發現並創造了數學。”他更喜歡公開聲稱的是，自己在數學上最大的成就是“發現了拉馬努金”。他在自己設計的一種關於天生數學才能的非正式的評分表中，給自己評了25分，給另一個傑出的數學家李特爾伍德評了30分，給他同時代最偉大的數學家希爾伯特（D. Hilbert）評了80分，而給拉馬努金評了100分。他甚至把拉馬努金的天才比作至少與數學巨人歐拉（L. Euler）和雅可比（C. Jacobi）相當。
斯里尼瓦瑟·拉馬努金
斯里尼瓦瑟·拉馬努金
斯里尼瓦瑟·拉馬努金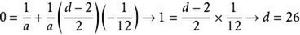
斯里尼瓦瑟·拉馬努金拉馬努金獨立發現公式： ，這個公式現在運用於超弦理論。 ,， ,， 維時空。
印度之子
為了激勵年輕人刻苦學習和奮發向上，馬德拉斯大學於1950年建立了一個用拉馬努金的名字來命名的高等數學研究所，並在研究所門前為他矗立一個大理石半身像；後來該所培養了不少優秀數學人才。印度人在紀念拉馬努金時，把他和聖雄甘地(M. Gandhi)、詩人泰戈爾(R. Tagore)等人一道，稱作“印度之子”。在1962年拉馬努金誕辰75周年之際，印度發行了一套紀念他的郵票。1975年印度成立了“拉馬努金學會”，1986年開始出版會刊。到1987年即拉馬努金誕辰100周年之際，印度已拍攝了3部有關他生平的電影。1987年在拉馬努金的故鄉馬德拉斯，當容納他最後一年心血的遺著《失散的筆記本》出版時，印度前總理甘地(R. Gandhi)親自趕去祝賀並參加了首發式。
美國佛羅里達大學於1997年創辦了《拉馬努金期刊》，專門發表“受到他影響的數學領域”的研究論文；該校還成立了一個國際性的拉馬努金數學會。千禧年時，《時代》周刊選出了100位20世紀最具影響力的人物，其中就有拉馬努金，並稱讚他是一千年來印度最偉大的數學家。現在國際上有兩項以拉馬努金命名的數學大獎，專門頒發給“與他有相同研究方向”的傑出青年數學家；已獲獎的華人數學家有洛杉磯加州大學教授陶哲軒、北京大學教授史宇光、北京清華大學訪問學者張偉和史丹福大學教師惲之瑋。
為紀念拉馬努金對數學的貢獻，印度總理辛格(M. Singh)於2012年2月26日宣布其誕辰為“印度數學日”（每年12月22日）及2012年為“印度數學年”。在拉馬努金誕辰125周年之際，印度舉辦了一系列紀念他的活動。美英等國的一些著名科學家在報上發表紀念文章，向拉馬努金表示崇高的敬意。《美國數學會志》在2012年12月號和2013年1月號上連續刊發紀念拉馬努金的系列文章，高度評價了他對數學作出的巨大貢獻。有趣的是，谷歌網站為紀念拉馬努金誕辰125周年專門繪了一張描述他少年學習情景的塗鴉。
值得一提的是，由於拉馬努金的傳奇色彩，世界上有多種關於他的傳記版本。其中麻省理工學院科學寫作教授卡尼格爾（R. Kanigel）1991年所著的《知無涯者：拉馬努金傳》（2008年被中國數學家、武漢大學前校長齊民友等翻譯成中文）最為成功，在美國成為暢銷書，並曾獲1992年“美國書評界傳記獎”。美國數學科普大師加德納（M. Gardner）對該書的評語是：“至今出版過的關於當代數學家的傳記中，這是最好的、文獻最豐富的作品之一……你一定會發現，對本世紀最傑出、謎一般的智者之一的光輝的研究會吸引住你。”
