歷史
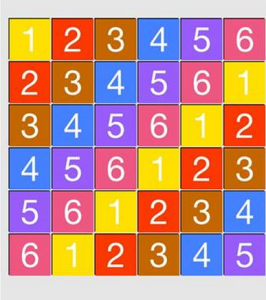 拉丁方陣
拉丁方陣後來,他去求教瑞士著名的大數學家歐拉。歐拉發現這是一個不可能完成的任務。來自n個部隊的n種軍銜的n×n名軍官,如果能排成一個正方形,每一行,每一列的n名軍官來自不同的部隊並且軍銜各不相同,那么就稱這個方陣叫正交拉丁方陣。歐拉猜測在
n=2,6,10,14,18,…時,正交拉丁方陣不存在。然而到了上世紀60年代,人們用計算機造出了n=10的正交拉丁方陣,推翻了歐拉的猜測。現在已經知道,除了n=2,6以外,其餘的正交拉丁方陣都存在,而且有多種構造的方法。
正交拉丁方陣
正交拉丁方陣的構造
請你造一個n=4的正交拉丁方陣。如果你有撲克牌,請用四種花色(梅花,方塊,紅心,黑桃)的1(即A)、2、3、4共16張牌,將它們排成4×4的方陣,每一行,每一列四種花色俱全,並且都有1、2、3、4。
正交拉丁方陣的特點
仔細欣賞一下,除了每行每列都有1、2、3、4,而且花色齊全。另外,這個圖還有許多特點:1. 一條對角線(從左上到右下)上全是A,另一條對角線(從左上到右下)上是試4。
2. 方塊與梅花是左右對稱的,紅桃與黑桃也是左右對稱的。就是說,如果沿中間的豎線將圖對摺,方塊與梅花相合,紅桃與黑桃相合。
3. 方塊與黑桃,梅花與紅桃上下對稱。就是說,如果沿中間的橫線將圖對摺,方塊和黑桃相合,梅花與紅桃相合。
4. A與4,2與3左右對稱。
5. 兩條對角線上四種四種花色齊全。
6. 方塊與紅桃中心對稱,黑桃與梅花中心對稱,就是說,如果將圖形繞中心(圖中橫線與豎線的點)鏇轉180°,左上的方塊與右下的紅桃相合。
上圖是另一種4階(n=4)的正交拉丁方陣,請同學們自己欣賞,發現一些規律和特點。學習數學,應當注意欣賞數學的美:整齊、對稱、有規律、簡單、自然、…。會欣賞數學的美才能將數學學的更好;學好了數學,也就提高了對數學美的認識。
判斷方法
拉丁方陣是一種n×n的方陣,方陣中恰有n種不同的元素,每種元素恰有n個,並且每種元素在一行和一列中 恰好出現一次。著名數學家和物理學家歐拉使用拉丁字母來作為拉丁方陣里元素的符號,拉丁方陣因此而得名。例如下圖是一個3×3的拉丁方陣:3 2 1
2 1 3
1 3 2
如果一個拉丁方陣的第一行和第一列按照元素的先後順序來排列,那么這稱為拉丁方陣的標準型,例如下 圖就是一個3x3的拉丁方陣標準型,第一行和第一列都是”1 2 3”。
1 2 3
2 3 1
3 1 2
【C語言】
//t=0時,不是拉丁方陣
//t=1時,是拉丁方陣
//t=2時,是標準型拉丁方陣

