抽象逼近
正文
在抽象空間中研究逼近論問題。設E是度量空間,ρ是E上的距離，對於確定的元x∈E和集G嶅E,量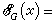
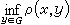為x與G的距離,它自然標誌著G對x的逼近程度，稱為G對x的最佳逼近值；使等式 ρ(x,y0)=EG(x)成立的元 y0∈G稱為 x在 G中的最佳逼近元。對最佳逼近值EG(x)的估計一般僅限於具體的E和G。抽象逼近主要研究下面三個問題：①最佳逼近元y0的存在性；②惟一性；③刻畫最佳逼近元的特徵。以上說的是集G對元x的逼近，有時給出一族被逼近元F=｛x｝,那么量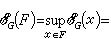
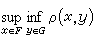就成了標誌逼近狀態的特徵量，稱EG(F)為集G對集F的最佳逼近值。有時需要在E的某子集族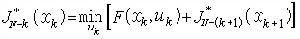
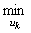中挑選最好的Gα，也即找出Gα0∈τ使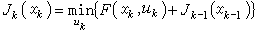
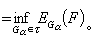
作為逼近集G，有時為E的線性子空間，這時的逼近稱為線性逼近；有時為E的凸子集,則稱為凸逼近。常見的凸逼近有:有界限逼近,係數有界限的多項式逼近，具有插值約束的逼近，共正逼近，共單調逼近等。
泛函分析是抽象逼近研究的主要工具。例如,若E為線性賦范空間，G是E的線性子空間，那么下述命題（哈恩—巴拿赫定理的推論）可用於導出最佳逼近估計和刻畫最佳逼近元的特徵：設x∈E\強，那么①
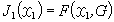
使得 ‖ƒ‖=1，ƒ(y)=0（對所有y∈G ），ƒ(x-y0)=‖x-y0‖。