定義
一組對邊相交的四邊形叫做折四邊形。
性質
邊
相同於一般的四邊形,任三邊之和大於第四邊。
對角線
對於兩條對角線都有:不在一條對角線的兩個頂點都在這條對角線的同一側。
角
關於折四邊形的內角,根本無法下一個嚴謹的概念,因此折四邊形的內角和就沒有意義了,唯一的可用的定理是:折四邊形ABCD中,若AD與BC相交,則∠A+∠B=∠C+∠D。
面積
類似於角,其面積也沒有嚴謹的定義,大多數將對邊相交形成的兩個三角形面積和作為其面積。
探討
為了對我們並不了解的折四邊形進行進一步了解,我們就儘可能的讓它符合一些四邊形的基本定理。
正因如此,這裡的內容可能和以上內容不符,個人認為,在下給出的定義只是為了使折四邊形更符合凹四邊形和凸四邊形罷了。
首先,先從四邊形內角和來看。根據角的定義,在本篇中,僅僅把射線順時針旋轉的角度來作為其角度值。
折四邊形abcd內角和為
 折四邊形內角和。
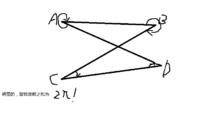
折四邊形內角和。2cπ(c為整數)有下圖可證。
這樣,輕易地我們就知道了,在構建折四邊形時,我們可以像右圖一樣,得出其內角和主值為2π。
即邊ab是通過負沿長得到的,根據有向線段的定義,ab為負值。若ad及bc都為正時,cd一定為正。
這樣我們要求折四邊形面積就簡單多了,因為其一邊為負,所以可以定義折四邊形面積為兩三角形面積之差,即正邊所構成三角形與負邊所在三角形面積的差。
當正邊所構成三角形比負邊所在三角形大時,為正,反之為非正。
個人認為,如果折四邊形如此定義邊角與面積,則會方便許多。
