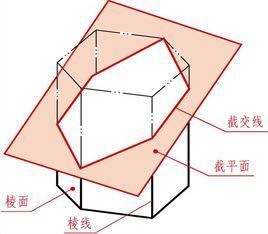
平面
平面,是指面上任意兩點的連線整個落在此面上,一種二維零曲率廣延,這樣一種面,它與同它相似的面的任何交線是一條直線 。是由顯示生活中(例如鏡面、平靜的水面等)的實物抽象出來的數學概念,但又與這些實物有根本的區別,既具有無限延展性(也就是說平面沒有邊界),又沒有大小、寬窄、薄厚之分,平面的這種性質與直線的無限延展性又是相通的。
截交線與截斷面
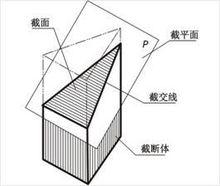 截平面
截平面截平面與立體表面的交線稱為截交線。截交線圍成的平面圖形稱為截斷面。
截平面的分類
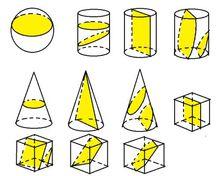 截平面
截平面截平面可分為橫截面、豎截面、平截面、直截面、斜截面等。
平面與迴轉體表面相交的特性
平面與迴轉體表面相交的截交線是由平面曲線、平面曲線和直線或由直線圍成的封閉線框,截交線的形狀與曲面立體的幾何性質及其與截平面的相對位置有關。平面與迴轉體表面相交的特性如下:
1.迴轉體的截交線的形式
通常截交線的形式取決於以下兩個方面:(1)迴轉體形狀;(2)截平面與迴轉體的相對位置。
2.截交線的性質
(1)截交線上的點既在截平面上又在迴轉體表面上,具有共有性。因此將這些共有點光滑地連線起來,便是截交線。
(2)截交線通常是一封閉的平面圖形,具有封閉性。
3.求截交線投影的作圖方法
(1)表面取點法:已知截交線的一個投影(有積聚性),利用表面取點法求出截交線的其他投影。
(2)輔助平面法:採用假設平面,使其與截平面和迴轉體表面相交,利用三面共有點的幾何原理,求出截交線上的一系列點,最後作出截交線的投影。
截平面的性質
截平面滿足一般平面的公理和推論
公理1 如果一條直線的兩個點在一個平面內,那么這條直線上的所有點都在這個平面內。
公理2 如果兩個平面有一個公共點,那么它們還有其他公共點,這些公共點的集合是一條直線。
公理3 經過不在一條直線上的三個點,有且只有一個平面。
推論一:經過一條直線和直線外的一點,有且只有一個平面。
推論二:經過兩條相交直線,有且只有一個平面。
推論三:經過兩條平行直線,有且只有一個平面。
截平面在加工中的套用
截面法加工的基本思想是:以一組平行平面或曲面切割加工表面,截出一系列交線,刀具與加工表面的切觸點沿這些交線運動,完成對曲面的加工。由於曲面與曲面求交比較困難,而平面和曲面求交算法效率高,可靠性好,所以截面多選擇平面,此時稱為截平面法。截平面法加工分為兩種:基於原曲面的截平面法和基於等距面的截平面法 。