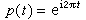概念
代數拓撲中的一個重要概念，又稱覆蓋空間。設p:塣→X是連續映射，如果在X中，每一點x都有開鄰域U,使得p-1(U)是塣中一組互不相交開集｛Uα｝的並集,且p 限制在每個Uα上都是從Uα到U 的同胚,則稱p 是復疊映射,塣是X 的一個復疊空間。 例如，由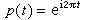
規定的直線到圓周的映射 p:E1→s1是復疊映射。設
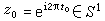,取正數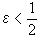
,作z0的開鄰域
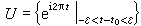,則p_1(U)是一組不相交開區間｛(n+t0-ε,n+t0+ε)｝的並集,且p:(n+t0-ε,n+t0+ε)→U是同胚。又如，當將n維球面Sn的每對對徑點粘合時，商空間是實射影空間Pn,粘合映射p:Sn→Pn也是復疊映射。 復疊映射的提升性質
復疊映射是一個纖維映射，即它對任何空間都有同倫提升性質（見同倫論）。此外，它還有更多的提升性質：映射提升定理
設Y連通、局部道路連通，y0∈Y，又設ƒ:Y→X 是連續映射，x0＝ƒ(y0)，取定慜0∈p_1(x0),則ƒ 有提升 愝: Y→塣 使 愝(y0)= 慜0 的充分必要條件是ƒ
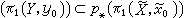。 映射提升惟一性定理
設Y連通,ƒ:Y→X是連續映射，ƒ的兩個提升愝,愝┡:Y→塣如果對某點y∈Y有愝(y)= 愝┡(y)，那么愝=愝┡。
用這兩個定理不難推出，當n>1時,復疊映射 p所誘導的同態p:πn(塣)→πn(X)是同構，而p:π1(塣)→π1(X)是單同態。
泛復疊空間
當P(π1(塣))是π1(X)的正規子群時,稱塣是X的正則復疊空間；如果塣是單連通的,則稱塣是X的泛復疊空間，它是最常用的復疊空間。
當一個拓撲空間X連通,局部道路連通與半局部單連通時，它一定存在泛復疊空間。
復疊變換群
是復疊空間塣 的自同胚群的一個子群，它由全體滿足p。φ =p的自同胚φ（稱為復疊變換）組成。
如果塣是泛復疊空間，並且X道路連通,則塣上的復疊變換群同構於π1(X),利用這個事實可計算某些空間的基本群。例如E1是S1的泛復疊空間,E1上的復疊變換就是移動距離是整數的平移，從而復疊變換群≌Z,這樣就得到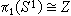
。又如n≥2時，Sn是Pn的泛復疊空間，復疊變換隻有兩個:恆同映射與對徑映射,於是
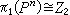。除了可用來計算基本群外，復疊空間在不動點理論的研究中是一種有效工具，並且在代數拓撲各個領域和幾何拓撲中還有廣泛的套用。
