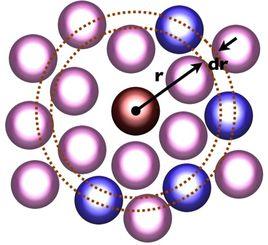
函式定義
徑向分布函式(Radial distribution function)通常指的是給定某個粒子的坐標,其他粒子在空間的分布幾率(離給定粒子多遠)。所以徑向分布函式既可以用來研究物質的有序性,也可以用來描述電子的相關性。
函式表示
徑向分布函式通常用g(r,r')來表示。
對 於|r-r'|比較小的情況,g(r,r')主要表征的是原子的堆積狀況及各個鍵之間的距離。對於長程的性質,由於對於給定的距離找到原子的幾率基本上相 同,所以g(r,r')隨著|r-r'|的增大而變得平緩,最後趨向於恆值。通常定義g(r,r')時,歸一化的條件為|r-r;|趨向於無窮大 時,g(r,r')趨向於一。通常,對於晶體,由於其有序的結構,徑向分布函式有長程的峰,而對於非晶體(amorphous)物質,則徑向分布函式一般只有短程 的峰。
同樣的概念有時被用到描述電子的相關性,如電子的對關聯(pair correlation)指的就是給定一個電子,其它電子在此電子周圍出現的幾率。由於電子之間有庫侖斥力,還有由於波函式反對稱化的作用,所以對關聯的具體形式比較複雜,目前尚未有解析的表達。有時候文獻里提到的exchange-correlation hole也是基於對關聯的概念。