正文
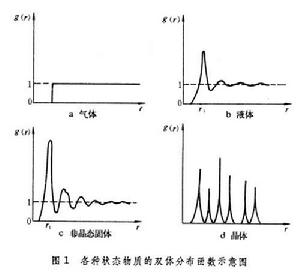
從原子間的相互作用以及其他約束條件出發,通過建造模型的方法得出某種可能的原子排列情況。非晶態材料的各種性質,是由它的微觀結構(包括原子結構和電子結構)決定的。目前對非晶態材料的電子結構了解很少,討論其結構常以原子結構為主。非晶態結構的主要特點,是長程無序、短程有序(見無序體系)。由於至今尚無任何技術可以準確測定,所以,利用結構模型是研究非晶態結構的一個重要方法。從模型可以得出各原子中心的坐標,分析原子分布的幾何特徵,討論其各種物理性能。將從模型推算出的材料性質與實驗觀測的結果進行比較。徑向分布函式F(r)表示以某個原子為中心,距離它r遠處單位厚度殼層中原子數的統計平均值,即F(r)=4πr2ρ(r),
式中ρ(r)是原子的數密度。有時也用雙體分布函式描述原子的分布,雙體分布函式g(r)是以某一原子的坐標作原點,距離它r遠處找到另一個原子的幾率
 非晶態材料的結構模型
非晶態材料的結構模型現在常用的非晶態結構模型有以下幾種。
微晶模型
認為非晶態材料的短程式與同成分的晶態材料相同,即非晶態是由極微小的晶粒組成的,晶粒大小約為十幾埃至幾十埃,各晶粒的取向的分布是散亂的。各種非晶態材料都可以採用這種模型。它可以定性地解釋非晶態材料的一些性質,如非晶態材料的密度常與晶態相近,衍射圖形成彌散的環。但是根據這種模型計算得到的F(r)或g(r)常與實驗符合得不很好,晶粒間界處原子的分布情況也不清楚。
與微晶模型近似的還有聚集團模型。各個聚集團有幾十個原子,有與晶體結構不同的短程式。聚集團不能像晶體元胞那樣連續填充空間,而是靠無規排列的原子相連線。
硬球無規密集排列模型
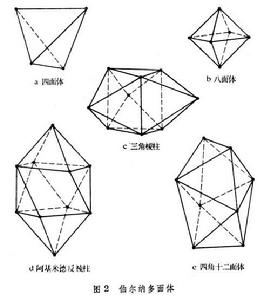
1959年J.D.伯爾納用等徑鋼球的堆積來模擬液體的結構。後來M.H.科恩等提出這樣得到的模型適於描述非晶態金屬的結構。建造這種模型時,把鋼球裝入器壁不規則或柔軟的容器中,加以振動或擠壓使之密集,將球粘結後再逐個剝下,測出各球心的坐標,就可以得出徑向分布函式和密度等數據。這些結果與實驗符合得較好。
伯爾納認為這種模型可以看作是由五種多面體組成的,一般稱之為伯爾納多面體(圖2)。分析模型中各種多面體的數量,知四面體有73%,而八面體很少,其餘幾種多面體有近似為五邊形的面。這些分析可以部分說明一些非晶態金屬結構的特徵。
 非晶態材料的結構模型
非晶態材料的結構模型1972年C.H.本涅脫用電子計算機建造硬球無規密集排列模型。結果是存儲在計算機內的一組球心坐標,當判據選擇合適時,所得的徑向分布函式與手工建造的模型很相近。利用計算機還可以模擬原子間的互作用,使硬球模型“鬆弛”。這樣可以使模型的徑向分布函式與實驗符合得更好。
連續無規排列模型
這種模型用一些細棒將代表原子的球連線起來,與每個球相連的細棒數等於球所代表的原子的價鍵數,細棒長度表示鍵長,細棒間的夾角表示鍵角。球和細棒組成的格線應能連續地填充空間,且不應出現晶態的長程周期性。模型內部應沒有或只有很少數一頭沒有與球相連的細棒(懸掛鍵),應力要小。這種模型常用來模擬靠共價鍵結合的非晶態半導體、氧化物玻璃等材料。所得的徑向分布函式一般與實驗符合較好。這種模型也可以用計算機建造,所得結果基本上與手工模型一致。
凍結氣體模型
電子計算機可以按照蒙特-卡羅法或分子動力學法模擬多原子體系,考察原子的分布狀況,計算出徑向分布函式。在高密度下,可以認為它是對非晶態固體結構的模擬。它模擬的是原子無規運動的瞬時情況,所以稱為凍結氣體模型。對於快速冷卻得到的非晶態金屬結構,這種模擬更直觀、更合理。當密度、溫度等參量選擇恰當時,所得的徑向分布函式與實驗符合得相當好。但是受計算時間等條件限制,一般只能作數十至數百個原子的模型。
通過對模型的考察和非晶態結構測定技術,人們已經對非晶態結構的主要特徵和概貌有了初步的了解。但是對非晶態結構細節的描述、各類的差別等方面還有大量工作要做。

