基本信息
如圖所示是一個彈簧振子的模型，其中金屬桿光滑，輕質彈簧質量遠小於金屬小球的質量，故可忽略不計。
| 位置 | A | A→ O | O | O→ B | B |
| 位移大小 | 最大 | 減小 | 0 | 增大 | 最大 |
| 速度大小 | 0 | 增大 | 最大 | 減小 | 0 |
| 動能 | 0 | 增大 | 最大 | 減小 | 0 |
| 勢能 | 最大 | 減小 | 0 | 增大 | 最大 |
| 總能 | 不變 | 不變 | 不變 | 不變 | 不變 |
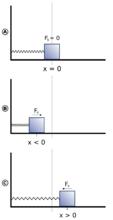彈簧振子在一個周期內位移、速度與回復力變化的示意圖。單擺也是一種理想化的模型，它的結構是一根輕質無彈性的細線一端懸掛（即細線的伸縮不計），另一端下系一小球，當小球的直徑遠小於線的長度，且小球的質量遠大於細線時，在不計空氣阻力的情況下，這樣的裝置叫單擺。當單擺的擺角小於等於5°，且在豎直平面內做往復運動時，所做的運動也是簡諧振動。小球是一個做簡諧振動的振子，意義和彈簧振子相同。
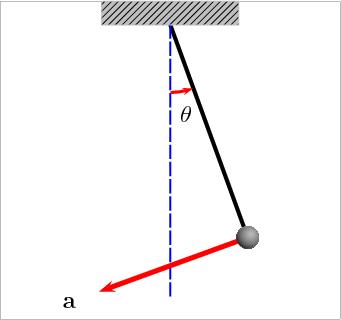單擺在一個周期內位移、速度與加速度變化的示意圖。
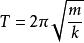彈簧振子彈簧振子的周期為。
其中k表示彈簧的勁度係數
m表示彈簧振子（小球）的質量。
推導過程
並不嚴格的方法
由簡諧振動位移公式 x=Asinωt （1）
對時間t求一次導數: v=Aωcosωt
再對時間t求一次導數:a=-Aω^2sinωt=-ω^2x （2）
再考慮簡諧振動的力的公式-kx=ma （3）
比較（1）、（2）、（3）三式（代入）
有-kAsinωt=-mAω^2sinωt
整理得ω^2=k/m
開方得ω=√(k/m)
則T=2π/ω=2π√(m/k)
用牛頓力學推飛彈簧振子運動方程
把坐標原點選在彈簧原長處，x軸沿彈簧方向，由牛頓第二定律
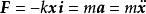彈簧振子在i方向投影后得到簡單的標量微分方程
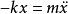彈簧振子這個微分方程的通解是
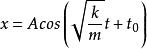彈簧振子我們就從理論上得出了位移公式，相比在“並不嚴格的方法”中直接給出的位移公式，是不是更加有說服力？
簡諧運動示意圖從三角函式的知識可知
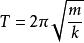彈簧振子用拉格朗日方法推飛彈簧振子運動方程
現在用分析力學的方法求解運動方程
先寫出拉格朗日函式
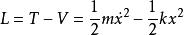彈簧振子把拉格朗日函式代入拉格朗日方程
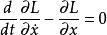彈簧振子即得
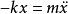彈簧振子