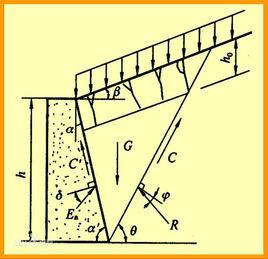
基本原理
庫倫於1776年根據研究擋土牆牆後滑動土楔體的靜力平衡條件,提出了計算土壓力的理論。他假定擋土牆是剛性的,牆後填土是無粘性土。當牆背移離或移向填土,牆后土體達到極限平衡狀態時,牆後填土是以一個三角形滑動土楔體的形式,沿牆背和填土土體中某一滑裂平面通過牆踵同時向下發生滑動。根據三角形土楔的力系平衡條件,求出擋土牆對滑動土楔的支承反力,從而解出擋土牆牆背所受的總土壓力。
計算
已知牆背AB傾斜,與豎直線的夾角為ε,填土表面AC是一平面,與水平面的夾角為β,若牆背受土推向前移動,當牆后土體達到主動極限平衡狀態時,整個土體沿著牆背AB和滑動面BC同時下滑,形成一個滑動的楔體△ABC。假設滑動面BC與水平面的夾角為α,不考慮楔體本身的壓縮變形。
取土楔ABC為脫離體,作用於滑動土楔體上的力有:①是牆對土楔的反力P,其作用方向與牆背面的法線成δ角(δ角為牆與土之間的外摩擦角,稱牆摩擦角);②是滑動面BC上的反力R,其方向與BC面的法線φ角(φ為土的內摩擦角);③是土楔ABC的重力W。根據靜力平衡條件W、P、R三力可構成力的平衡三角形。利用正弦定理,得:P/[sin(α-φ)]=W/sin[180°-(ψ+α-φ)]
所以 P=[Wsin(α-φ)]/[sin(ψ+α-φ)] (1)
其中 ψ=90°-(δ+ε)
假定不同的α角可畫出不同的滑動面,就可得出不同的P值,但是,只有產生最大的P值的滑動面才是最危險的假設滑動面,與P大小相等、方向相反的力,即為作用於牆背的主動土壓力,以Pa表之。
對於已確定的擋土牆和填土來說,φ、δ、ε和β均為已知,只有α角是任意假定的,當α發生變化,則W也隨之變化,P與R亦隨之變化。P是α的函式,按 dP/dα=0的條件,用數解法可求出P最大值時的α角,然後代入式(1)求得主動土壓力