靜止壓力
擋土牆完全沒有側向位移、偏轉和自身彎曲變形時，作用在其上的土壓力即為靜止土壓力，此時牆后土體處於側限應力狀態（彈性平衡狀態），與土的自重應力狀態相同。 半無限土體中z深度處一點的應力狀態，巳知其水於面和豎直面都是主應力面。作用於該土單元上的豎直向主應力就是自重應力σv=γz，則水平向自重應力（靜止土壓力強度）： σ= σ=kγz
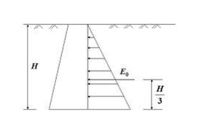圖1 靜止土壓力分布式中——k土的側壓力係數或靜止土壓力係數，對於正常固結粘性土，可近似按k≈1-sin j’（Jaky，1944)，（j’為土的有效內摩擦角）。
γ ——牆後填土重度。
靜止土壓力強度分布沿牆高呈三角形分布。若牆高為H，則作用於單位長度牆上的總靜止土壓力Eo為 ：Eo的作用點應在牆高的1/3處。
庫倫壓力
計算理論
庫倫土壓力理論是根據牆后土體處於極限平衡狀態並形成一滑動楔體時，從楔體的靜力平衡條件得出的土壓力計算理論。
基本假設 ：
① 牆後的填土是理想的散粒體(粘聚力c=0)；
② 牆背傾斜、粗糙、牆後填土面傾斜；
③ 滑動破壞面為一平面（牆背AB和土體內滑動面BC）；
④ 剛體滑動。不考慮滑動楔體內部的應力和變形條件；
⑤ 楔體ABC整體處於極限平衡狀態。在AB和BC滑動面上，抗剪強度均巳充分發揮。即剪應力τ均已達抗剪強度τ。
圖2 柔性擋土牆的土壓力
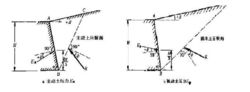圖3 剛性擋土牆的土壓力主動計算
圖3一剛性擋土牆，牆高為H，牆背AB的傾斜角為α，填土頂面坡度為β，填料為砂土，其單位重為γ，內摩擦角為ψ，牆背摩擦角為δ。若牆背AB在土壓力作用下向左移動，使土體的側壓力減小而發生破壞，破壞時產生一個處於極限平衡狀態的滑動土楔體ABC，此時牆背所受的土壓力稱為主動土壓力E（圖a）。反之，如果牆背AB在外力作用下向右移動，並使土體的側壓力增大而發生破壞，也產生一個處於極限平衡狀態的滑動土楔體ABC，而牆背所受的土壓力稱為被動土壓力E（圖b）。如圖上所示，被動土壓力大於主動土壓力。土體破裂面BC一般呈曲線狀。為了簡化計算，C.-A.de庫侖假設破裂面為直線，並據此導出下列計算土壓力公式：
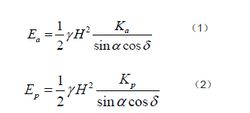土壓力式中γ為土的容量；Ka和Kp分別為主動土壓力係數和被動土壓力係數：
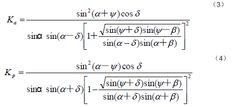土壓力如果牆壁垂直且光滑，填土表面為水平，即α=90°，β=δ=0，式（3）、（4）變為：
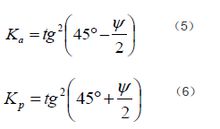土壓力這種情況稱為蘭金狀態。上述庫侖和蘭金理論均假定土壓力的分布規律為三角形，其合力作用點在牆背高度的1/3處。
蘇聯B. B. 索科洛夫斯基用極限平衡理論求出具有任何填土表面的傾斜擋土牆土壓力的精確解答，他求得的滑動破裂線都是對數螺鏇曲線。對於牆後有水平填土表面的垂直剛性擋土牆，用庫侖和蘭金理論所得的結果與索科洛夫斯基的精確解答大致有如下關係：
E=1.24E，
E=0.98E，
式中E為按蘭金理論計算的結果；E為按庫侖理論計算的結果；E為按精確方法計算的結果。由此可知，確定擋土牆主動土壓力時，用庫侖理論能得出足夠精確的結果。但據一些學者的實驗研究，用庫侖理論確定被動土壓力，誤差較大，而且這個誤差還隨著土的內摩擦角的增大而增大。
朗肯壓力
依據
朗肯土壓力理論是根據半空間體的應力狀態和土的極限平衡理論得出的土壓力計算理論之一。
基本假設：牆背直立、光滑，牆後填土面水平。 這時，牆背與填土界面上的剪應力為零。不改變右邊土體中的應力狀態。當擋土牆的變位符合上述主動或被動極限平衡條件時，作用在擋土牆牆背上的土壓力即為朗肯主動土壓力或朗肯被動土壓力。
計算
（1）主動土壓力計算
土的極限平衡條件：土體處於極限平衡狀態時土的應力狀態和土的抗剪強度指標之間的關係式。
大主應力σ = σ=γz
小主應力σ = σ
主動土壓力強度σ = σ
粘性土
無粘性土
主動土壓力係數
粘性土的主動土壓力強度包括兩部分：
1.由土自重引起的土壓力γzKa；
2.由粘聚力c引起的負側壓力2cKa1/2。
其中負側壓力對增背是拉應力，實際上牆與土在很小的拉力作用下就會分離（一般情況下認為土不能承受拉應力），故在計算土壓力時，這部分應忽去不計。
臨界深度z
粘性土主動土壓力作用點位於牆底以上（H - z)/3處
無粘性土主動土壓力，E— 合力（集中力），作用點位於牆底以上H /3處
（2）被動土壓力計算
土的極限平衡條件
大主應力σ = σ
小主應力σ = σ=γz
被動土壓力強度σ = σ
粘性土
無粘性土
被動土壓力係數
粘性土被動土壓力
E方向垂直牆背，作用點位於梯形面積的重心上
非粘性土被動土壓力
E方向垂直牆背，作用點位於作用點位於牆底以上H /3處
比較
一、朗肯與庫倫土壓力理論均屬於極限狀態土壓力理論。用這兩種理論計算出的土壓力都是牆后土體處於極限平衡狀態下的主動與被動土壓力。
二、兩種分析方法上存在的較大差別，主要表現在研究的出發點和途徑的不同。朗肯理論是從研究土中一點的極限平衡應力狀態出發，首先求出的是作用在土中豎直面上的土壓力強度sa或sp及其分布形式，然後再計算出作用在牆背上的總土壓力Ea和Ep，因而朗肯理論屬於極限應力法。庫倫理論則是根據牆背和滑裂面之間的土楔，整體處於極限平衡狀態，用靜力平衡條件，先求出作用在牆背上的總土壓力Ea或Ep，需要時再算出土壓力強度sa或sp及其分布形式，因而庫倫理論屬於滑動楔體法。
三、上述兩種研究途徑中，朗肯理論在理論上比較嚴密，但只能得到理想簡單邊界條件下的解答，在套用上受到限制。庫倫理論顯然是一種簡化理論，但由於其能適用於較為複雜的各種實際邊界條件，且在一定範圍內能得出比較滿意的結果，因而套用廣泛。
四、朗肯理論的套用範圍：牆背垂直、光滑、牆後填土面水平，即a= 0，b= 0，d= 0。無粘性土與粘性土均可用。庫倫理論的套用範圍：用於包括朗肯條件在內的各種傾斜牆背的陡牆，填土面不限，即a，b，d可以不為零或等於零，故較朗肯公式套用範圍更廣。數解法一般只用於無粘性土，圖解法則對於無粘性土或粘性土均可方便套用。
五、計算誤差
朗肯和庫倫土壓力理論都是建立在某些人為假定的基礎上，朗肯假定牆背為理想的光滑面，忽略了牆與土之間的摩擦對土壓力的影響，庫倫理論雖計及牆背與填土的摩擦作用，但卻假定土中的滑裂面是通過牆鍾的平面，與比較嚴格的擋土牆土壓力解（按極限平衡理論，考慮d，土體內的滑裂面是由一段平面和一段對數螺線曲面所組成的複合滑動面求得），計算結果都有一定的誤差。
對於主動土壓力計算，各種理論的差別都不大。朗肯土壓力公式簡單，且能建立起土體處於極限平衡狀態時理論破裂面形狀和概念。在具體實用中，要注意邊界條件是否符合朗肯理論的規定，以免得到錯誤的結果。庫倫理論可適用於比較廣泛的邊界條件，包括各種牆背傾角、填土面傾角和牆背與土的摩擦角等，在工程中套用更廣。被動土壓力的計算、當d和j較小時，這兩種古典土壓力理論尚可套用；而當d和j較大時，誤差都很大，均不宜採用。
其他計算
確定土壓力還有圖解分析法和圖解法。圖解分析法是用作圖確定近似於滑動線的精確曲線，然後確定滑落稜體各部分的重量，藉助力的三角形，求出土壓力的數值。圖解法是以庫侖假設為基礎，即假設滑動線為直線，此法一般僅適用於確定主動土壓力，結果同精確解相近。確定被動土壓力則必須採用圖解分析法。圖解法和圖解分析法的優點在於能自行核對，避免較大誤差，可以用簡便的作圖方法計算複雜條件下的土壓力。
有地下水位時土壓力的計算
地下水位對土壓力的影響，具體表現在：
(1) 地下水位以下填土重量將因受到水的浮力而減小．計算土壓力時套用浮容重γ；
(2) 地下水對填土的強度指標c、j的影響。一般認為對砂性土的影響可以忽略；但對粘性填土，地下水將使c、j值減小．從而使土壓力增大；
(3) 地下水對牆背產生靜水壓力作用。
土壓力水土合算→粘性土
水土分算→無粘性土
連續均布荷載作用下土壓力計算
地表連續均布荷作用下，作用在牆背面的土壓力強度sa由兩部分組成：一部分由均布荷載q引起（常數），其分布與深度z無關; 另一部分由土重引起，與深度z成正比。總土壓力E即為梯形分布圖的面積。
地表局部荷載作用下土壓力計算
填土表面有局部荷載q作用下，則q對牆背產生的附加土壓力強度值仍可用朗肯公式計算，即sa=qKa ，但其分布範圍缺乏在理論上的嚴格分析。一種近似方法認為，地面局部荷載產生的土壓力是沿平行於破裂面的方向傳遞至牆背上的。
牆背設定卸荷平台時土壓力計算
為了減少作用在牆背上的主動土壓力．有時採用在場背中部加設卸荷平台的辦法。此時，平台以上Hl高度內，可按朗肯理論，計算作用在AB面上的土壓力分布。由於平台以上土重W已由卸荷台BCD承擔，故乎台下C點處土壓力變為零，從而起到減少平台下H2段內土壓力的作用。減壓範圍，一般認為至滑裂面與牆背交點E處為止。連線圖中相應的C和E，則圖中陰影部分即為減壓後的土壓力分布。顯然卸荷平台伸出越長，則減壓作用越大。
