簡介
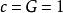幾何化單位制幾何化單位制（geometrized unit system），不是一種完全定義或唯一的單位制。在這單位制內，只規定光速與重力常數為1，即。這樣留出足夠空間來規定其它常數，像波茲曼常數或庫侖常數：
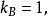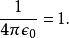幾何化單位制
幾何化單位制
幾何化單位制假若約化普朗克常數也規定為，則幾何化單位制與普朗克單位制完全相同。
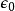幾何化單位制
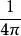幾何化單位制
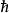幾何化單位制另外，我們也可以不定義庫侖常數為1，而改定義更自然的電常數為1，此時，庫侖常數就會變成，這是比較自然的有理化幾何單位制，而如果是定義庫侖常數為1，則是非理化的幾何單位制。（我們通常會選擇比較自然的常數定義為1，例如我們不會把原始的普朗克常數h定義為1，而是會把約化普朗克常數定義為1，因為約化普朗克常數比較自然）。
相對論中的幾何化單位制
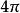幾何化單位制在廣義相對論中，G經常會與合併，故此時的幾何單位制定義為：
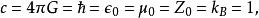幾何化單位制
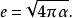幾何化單位制 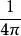幾何化單位制注意此時的萬有引力常數與庫侖常數的值相同，都是。
普朗克單位制
普朗克單位制是一種計量單位制度，由德國物理學家馬克斯·普朗克最先提出，因此命名為普朗克單位制。這種單位制是自然單位制的一個實例，經過特別設計，使得某些基礎物理常數的值能夠簡化為1。在統一理論方面的研究，特別如量子引力學中，普朗克單位制能夠給研究者一點大概的提示。
參閱
•普朗克單位制
