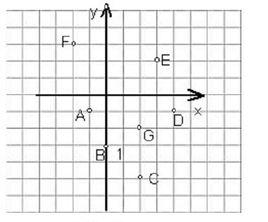
定義
定義一
坐標縱軸為x,自原點向北為正;坐標橫軸為y,自原點向東為正。點的平面坐標為(x,y)。選任意子午線為坐標縱軸和高斯投影面的坐標系或選高斯-克呂格投影分帶的中央子午線為縱軸和任意高程面的坐標系,則屬於地方(礦區)平面坐標系。如果任意選定坐標原點和x軸方向,則稱獨立平面坐標系。
在平面坐標系統中,由已知點A (xA,yA)計算未知點B的坐標稱坐標正算 (見圖),按下式計算:
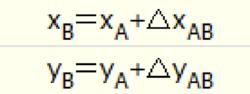平面坐標式中△x和△y是點B對點A的坐標增量,可按下式計算:
△x=Scosα
△y=Ssinα
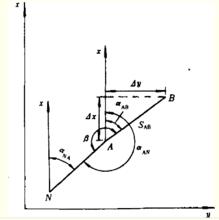
式中S是直線AB的水平投影長度;α是AB邊方向的坐標方位角,可根據已知的方位角α和測得的水平角β計算,α=α+β=α±180°+β,β定義為方位角推算方向左側的水平角。
坐標計算
平面坐標根據兩點平面坐標計算坐標方位角和邊長,稱坐標反算。若已知A、B兩點坐標(x,y)和(x,y),則可得:
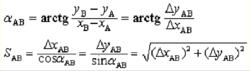平面坐標定義二
平面幾何的基本概念之一.指空間中表示平面位置的有序數組.例如,在空間中,若空間中點的齊次坐標用(x,x,x,x)表示,則平面π:ux+ux+ux+ux=0由它的係數u,u,u,u所決定.有序四數組{u,u,u,u}稱為平面的齊次坐標,記為π[u,u,u,u].平面的齊次坐標適合下列條件:
1.不全為零的有序四數組[u,u,u,u]表示一個平面.
2.成比例的有序四數組[u,u,u,u]與[ρu,ρu,ρu,ρu](ρ≠0)表示同一個平面.
3.P(x′,x′,x′,x′)在平面π[u,u,u,u]上的充分必要條件為
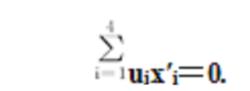平面坐標相關計算
在平面坐標系統中,由已知點A (xA,yA)計算未知點B的坐標稱坐標正算 (見圖),按下式計算:
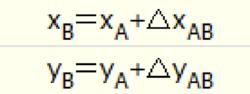平面坐標式中△x和△y是點B對點A的坐標增量,可按下式計算:
△x=Scosα
△y=Ssinα
式中S是直線AB的水平投影長度;α是AB邊方向的坐標方位角,可根據已知的方位角α和測得的水平角β計算,α=α+β=α±180°+β,β定義為方位角推算方向左側的水平角。
坐標計算
平面坐標根據兩點平面坐標計算坐標方位角和邊長,稱坐標反算。若已知A、B兩點坐標(x,y)和(x,y),則可得:
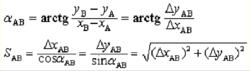平面坐標