平移作圖

平移（translation）是指在平面內，將一個圖形沿著某個方向移動一定的距離，這樣的圖形運動叫做平移[1]，平移不改變物體的形狀和大小。

定義

它是等距同構，是仿射空間中仿射變換的一種。它可以視為將同一個向量加到每點上，或將坐標系統的中心移動所得的結果。即是說，若是一個已知的向量，是空間中一點，平移。

將同一點平移兩次，結果可用一次平移表示，即，因此所有平移的集是一個群，稱為 平移群。這個群和空間同構，又是歐幾里德群E(n)的正規子群。

性質

經過平移，對應線段平行（或共線）且相等，對應角相等，對應點所連線的線段平行且相等；

平移變換不改變圖形的形狀、大小和方向(平移前後的兩個圖形是全等形)。

例題

（1） △ABC按箭頭方向移動三厘米的圖。

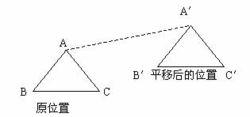圖1

結果：如圖1

（2)圖2可看作是由什麼圖形平移得到的？

圖2

結果：由一個小圖形得到的。