右平移

右平移是半群上的一類特殊變換。半群 S 上的一個變換 ρ(λ) ，若對任意x,y∈S，有 x(yρ)=(xy)ρ，(λx) y = λ(xy)，則稱 ρ(λ) 為 S 的右（左）平移。

半群中的右平移

右平移是半群上的一類特殊變換。

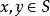右平移

半群 S 上的一個變換 ρ(λ) ，若對任意，有 x(yρ)=(xy)ρ，(λx) y = λ(xy)，則稱 ρ(λ) 為 S 的右（左）平移。

右平移

右平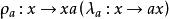移

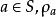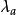右平移

右平移

半群 S 上的一個右平移 ρ 與一個左平移 λ ，若對任意有 x(λy)=(xρ)y ，則稱 ρ 與 λ 是環結的；若a∈S，則 S 上的變換是右（左）平移，這類右（左）平移稱為半群 S 的內右（左）平移，關於任意與是環結的。

李群李代數中的右平移

李群李代數 (Lie algebra of Lie group) 是由李群產生的相應的李代數。

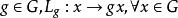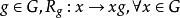右平移

右平移

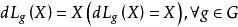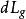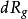若 G 為李群（實或復），則任取 為 G 之雙解析同胚，稱為 G 的左平移，任取 為 G 之雙解析同胚，稱為 G 的右平移。

右平移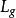

右平移

右平移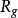

右平移

右平移

若 G 上向量場 X 滿足（和分別是 和 的微分），則稱 X 為左（右）不變的，G 上所有左（右）不變向量場構成 dim G 維李代數，G 上所有左（右）不變向量場構成的李代數稱為李群 G 的李代數。