定義
圖（一）空間區域V及在V內的球面S若在一個空間區域V內，電位 Φ( r)處處滿足拉普拉斯方程，即 ▽² Φ( r)=0，則V內任一點的電位值都等於V內以該點為球心的球面上的電位值的平均值。這就是說，對於如圖所示的空間區域V，若在V內有 ▽² Φ( r)=0，S是以P點為球心，半徑為R的球面，則P點的電位值
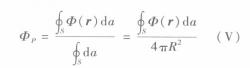1這裡，球面S的半徑R可以是任意數值，只要保證S在V內即可 。
定理的證明
格林(Green)定理
為了證明平均值定理 ，需要使用數學上的格林定理(亦稱格林恆等式或格林公式)。下面來敘述格林定理的內容。
如果標量函式f（ r）和Ψ( r)在一個體積V及V的表面S上是良態的，則下列等式成立
2兩式分別稱為格林第一和第二定理(恆等式、公式)。
格林定理的證明是很簡單的，只要令 A=ψ▽f，並使用高斯定理式等，即可得。
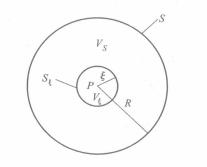圖（二）球面S將圖中的球面S放大，為了證明的方便，將坐標原點定在P點。由於P點的任意性，證明不失一般性。這樣，S即是rs=R的球面，S所包同的全部體積為Vs。使用格林第二定理式將式中的標量函式f( r)用標量位Φ( r)代人，即取f= Φ，由於在所討論的區域內， Φ滿足拉普拉斯方程， ▽² Φ( r)=0，因此可得
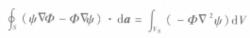3選取
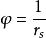平均值定理
平均值定理但是 在P點不收斂，為了符合格林定理的條件，從Vs中挖出一個小塊Vξ，它是以P點為球心，ξ為半徑的球面Sξ所包同的小球體。這樣代人3式，改變積分域，則可得
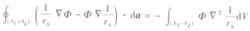4 平均值定理而在區域（Vs-Vξ）中 ▽² =0
這樣就有
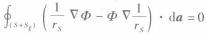5注意到式4和式5中，Sξ法線方向是（- irs）方向，若將S和Sξ上所做的積分分開計算，則Sξ的法線方向應改為( irs)方向。因此由式5可得
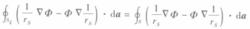6注意到在S ξ上有rs=ξ，所以
7這裡使用了高斯定理，並且考慮到 Φ滿足拉普拉斯方程。同理可得
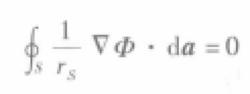8這樣，式6還餘下兩項，先研究一下該式右邊的一項。由於
9而在S上，rs= R，d α= irsdα，因此
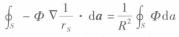10再研究一下式6左邊剩下的一項。注意到在Sξ上，rs=ξ，考慮到式9並使用積分中值定理，則可得
11
12式中，P’為Sξ上的某一點。
最後，再令ξ→0，取極限。由於
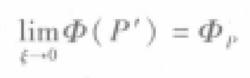13這樣，綜合上面各式的結果就可得
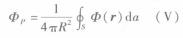14這就是平均值定理式(1)。
另外，還可以使用δ函式來證明平均值定理 。
套用
平均值定理在理論研究上是很有用的。另外，它還可以用在近似計算上，從而可以使州計算機對那些不能求得解析解的系統求得其數值解 。在做近似計算時，我們是用若干離散點上的電位值之和來代替式(14)中的積分值，而以離散點的個數來代替球面面積的。這是因為在圖（一）中，若我們在S上取n個點，每個點的電位分別為Φsr,可得
15如果已知的系統是與某一維，例如與z坐標無關，則問題化為二維問題。這時平均值定理就化為
16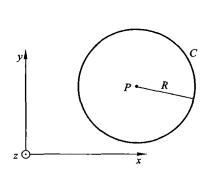
圖（三）以P點為圓心的圓周C
圖（四）無限長接地金屬槽式中，C是以P點為圓心的圓周，圓周半徑為R，如圖(三)所示。
若在C上取n個點，各點電位為ΦCi,則近似計算公式即為
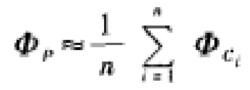17例如對於圖(四)所示的一個無限長接地金屬槽，若槽口電位為V0，即可使用式(17)求得槽內的電位數值分布。
首先，如圖所示將槽的橫截面分成很多小正方形的格線，再對所有的交點，如圖上P點、1點、2點、3點、4點等等都賦予一個假定的電位值，作為問題的零階數值解。然後將零階解代人式(17)中，求出各點的新的電位值，作為一階數值解。例如圖中
18再經過同樣運算，將一階數值解代人式(17)求得二階數值解。這樣不斷進行下去，直到所得的解滿足我們允許的誤差時，即可停止運算，從而得到滿意的數值解。這種近似求解的方法就是數值解法中常用的疊代法。而用數值法求解靜電場的理論基礎就是平均值定理 。
