簡介
關於隨機變數列在一定收斂意義下收斂於某隨機變數的定理的總稱,包括大數定律、小數定律、中心極限定理、局部極限定理等。
隨機變數、分布函式列(機率分布列、特徵函式列……)在一定意義下收斂於某隨機變數、分布函式(機率分布、特徵函式……)的有關定理的總稱,主要包括大數定律、小數定律、重對數定律、中心極限定理、局部極限定理……
以大數定理和中心極限定理為核心的極限定理是機率論的基本理論之 一,它們在機率論與數理統計的理 論研究與套用中都具有十分重要的意義。
大數定律定義
在機率論中,用來闡明大量平均結果穩定性的一系列定理統稱為大數定律。
中心極限定律定義
在客觀實際中有許多隨機變數,它們是由大量相互獨立的隨機因素的綜合效應所形成的,而其中的每一個單個因素在總的效應中所起的作用都是微小的。這類隨機變數往往近似地服從常態分配。在機率論中,論證隨機變數和的極限分布是常態分配的一系列定理統稱為中心極限定理。
定理
切比雪夫不等式
 極限定理
極限定理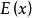 極限定理
極限定理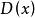 極限定理
極限定理 極限定理
極限定理設隨機變數 有數學期望和方差,則對於任意給定的正數,總成立不等式
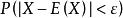 極限定理
極限定理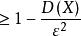 極限定理
極限定理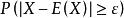 極限定理
極限定理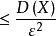 極限定理
極限定理或
此不等式稱為切比雪夫不等式。
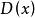 極限定理
極限定理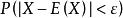 極限定理
極限定理 極限定理
極限定理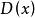 極限定理
極限定理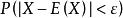 極限定理
極限定理 極限定理
極限定理由切比雪夫不等式可以看出,若方差越小,則機率越大,表明隨機變數 取值越集中;反之,方差越大,機率越小,表明隨機變數 取值較分散。
大數定律
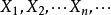 極限定理
極限定理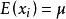 極限定理
極限定理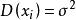 極限定理
極限定理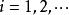 極限定理
極限定理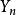 極限定理
極限定理定理1(切比雪夫定理的特殊情況)設隨機變數相互獨立,且具有相同的有限數學期望和方差:,()。作前n 個隨機變數的算術平均,記為
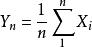 極限定理
極限定理 極限定理
極限定理即,則對於任意正數,
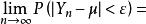 極限定理
極限定理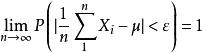 極限定理
極限定理恆有
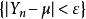 極限定理
極限定理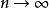 極限定理
極限定理 極限定理
極限定理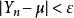 極限定理
極限定理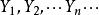 極限定理
極限定理 極限定理
極限定理式中,是一個隨機事件,等式表明,當時,這個事件的機率趨於1,即對於任意正數,當n 充分大時,不等式幾乎都是成立的。通常我們稱序列依機率收斂於。
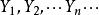 極限定理
極限定理 極限定理
極限定理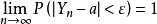 極限定理
極限定理一般地,設為一個隨機變數序列,a 是一個常數,若對於任意正數都有
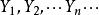 極限定理
極限定理則稱隨機變數序列依機率收斂於a 。
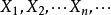 極限定理
極限定理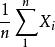 極限定理
極限定理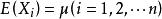 極限定理
極限定理定理1 表明,當n 很大時,隨機變數的算術平均接近於數學期望,這種接近是機率意義下的接近。
證明方法
這個大數定律的證明確實有幾種不同的方法。最早的證明是由數學大師Kolmogorov給出的。Durrett (2010)的書上用的是Etemadi (1981)的方法,需要截斷X,用到現代機率論的知識如Borel-Cantelli引理、Kolmogorov三級數定理、Fubini定理等。(感謝讀者指出,Durrett的書在倒向鞅一章中給出了大數定律的倒向鞅方法證明,只需要用到倒向鞅的知識和Hewitt-Savage 0-1律,不過這也是現代機率論的知識。)
此外,還有很多不同的大數定律,不同分布的,不獨立的序列等。定律也不一定是關於隨機變數的,也可以是關於隨機函式的,甚至隨機集合的等等。以數學家命名的也有Khinchin大數定律(不獨立序列的強大數定律)、Chebyshev大數定律(弱大數定律(1))、Poisson大數定律(不同機率的隨機事件序列的大數定律)、Bernoulli大數定律(隨機事件的大數定律)、Kolmogorov大數定律(強大數定律(6))等等……
中心極限定理
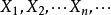 極限定理
極限定理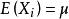 極限定理
極限定理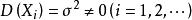 極限定理
極限定理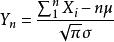 極限定理
極限定理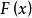 極限定理
極限定理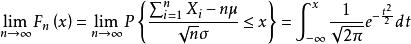 極限定理
極限定理定理2 (同分布的中心極限定理)設隨機變數相互獨立,服從同一分布並且具有有限的數學期望和方差,,則隨機變數的分布函式對任意的x,滿足
在很多問題中,所考慮的隨機變數,都可表示成若干獨立的隨機變數之和。它們往往近似地服從常態分配。在後面將學的數理統計中,我們會看到,中心極限定理是大樣本統計 推斷的理論基礎。
套用
中心極限定理是機率論中最重要的一類定理,它支撐著和置信區間相關的T檢驗和假設檢驗的計算公式和相關理論。如果沒有這個定理,之後的推導公式都是不成立的。
事實上,以上對於中心極限定理的兩種解讀,在不同的場景下都可以對A/B測試的指標置信區間判定起到一定作用。
對於屬於常態分配的指標數據,我們可以很快捷地對它進行下一步假設檢驗,並推算出對應的置信區間;而對於那些不屬於常態分配的數據,根據中心極限定理,在樣本容量很大時,總體參數的抽樣分布是趨向於常態分配的,最終都可以依據常態分配的檢驗公式對它進行下一步分析。
總結
綜上所述,通俗的說,大量隨機變數的平均值已不具有顯著的隨機性,而是必然接近 某個常數,這是自然界一類隨機現象隱含 的最重要的規律之一;另一規律是,儘管 個別隨機變數的分布函式可能各式各樣, 但大量相互獨立的隨機變數和的分布不再 是任意的,而是服從常態分配。