定義式
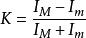干涉條紋對比度
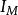干涉條紋對比度
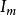干涉條紋對比度其中、分別是條紋光強的極大值和極小值。
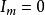干涉條紋對比度
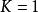干涉條紋對比度
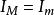干涉條紋對比度
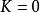干涉條紋對比度從定義式來看，條紋的對比度與亮暗條紋的相對光強有關。當時，，對比度最好，稱為完全相干；當時，，條紋完全消失，為非相干。
光源大小的影響
光源臨界寬度
臨界寬度即為對比度下降到零時光源的寬度。
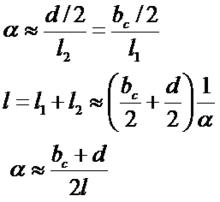干涉條紋對比度
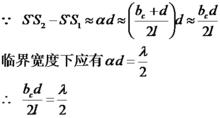干涉條紋對比度條紋對比度隨光源大小的變化
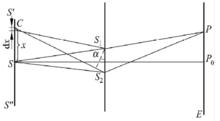干涉條紋對比度
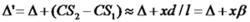干涉條紋對比度若用Δ表示S點的元光源通過s1、S2到達P點的光程差，則
因此，由C處的元光源在P點產生的干涉光強為
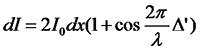干涉條紋對比度寬度為b的擴展光源S’S’’在P點產生的干涉場平均強度為
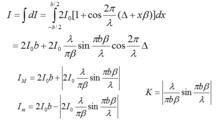干涉條紋對比度一般認為，當光源寬度不超過臨界寬度的四分之一時，條紋的對比度是良好的。這個光源寬度稱為許可寬度度bp。
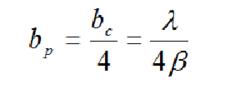干涉條紋對比度
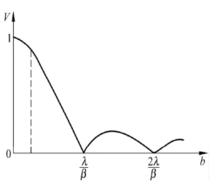干涉條紋對比度空間相干性
若擴展光源S’S’’發出的光通過小孔S1、S2後再度複合時能夠產生干涉，則稱通過空間這兩點的光具有空間相干性。
光波的空間相干性與光源大小密切相關。當光源的寬度小於臨界寬度時，光波才具有相干性。
當光源寬度為臨界寬度時，有b=λl/d。
此時，通過S1和S2兩點的光不發生干涉，因而沒有空間相干性。定義該情況下S1和S2兩點之間的距離為橫向相干寬度，以dt表示，dt=λl/b。
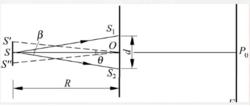干涉條紋對比度或以擴展光源S1、S2對O點的張角θ表示，dt=λ/θ。
產生干涉的兩光源之間的距離必須小於橫向相干寬度才能產生干涉條紋。現有光源中空間相干性最好的是雷射。
如果擴展光源是方形的（在垂直於圖面的方向上寬度也是b），則它照明的平面上相干範圍的面積（相干面積）為：
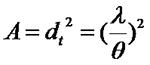干涉條紋對比度如果擴展光源是圓形的：
dt= 1.22λ/θ
相干面積：
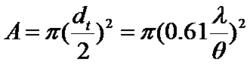干涉條紋對比度光源非單色性的影響
儘管在各種干涉實驗中我們使用了單色光源，但任何一種光源都不可能是絕對單色的，即光源發出的光波不可能是單一波長的，都會有一定的波長變化範圍Δλ。
由於在Δλ變化範圍內的每一種波長的光都各自產生一組干涉條紋，而除零級以外的各級條紋間都發生位移、重疊，所以最終的情況將使得條紋的對比度下降，因此需要對光源非單色性的影響進行討論。
相干長度
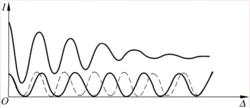
下圖顯示了波長為λ和λ+ Δλ的兩光波的干涉強度曲線，圖中上部為疊加後總的強度曲線。
由兩組曲線可看出，兩組不同波長的條紋的相對移動量隨著光程差δ的增大而增大，總強度曲線中的最大、最小值之差也隨光程差增大而變小，最終將趨於零。
干涉條紋對比度由此可知，在這種情況下，要產生清晰的條紋，即要使條紋的對比度在允許的範圍內，需要對干涉時的光程差進行限制。
定義能夠產生干涉時的最大光程差為相干長度δ max。
設單色光源的波長為λ，波長的變化範圍為Δλ，則波長為λ+ Δλ的第m級條紋和波長為的第m+1 級條紋位置重合時的光程差就是相干長度:
δ max=（m+1)λ=m（λ+Δλ）
條紋對比度為零時干涉級數為：m=λ/Δλ。
相干長度為：δ max=λ²/Δλ。
由相干長度的表達式可知，相干長度與光波的變化範圍即光譜寬度成反比，即光源的單色性越好，Δλ 越小，則越容易實現干涉。兩光波干涉時所能允許的最大光程差為波列的長度。
條紋對比度與Δλ和λ的關係
由上面的分析已得出了光源的光譜寬度Δλ會使干涉條紋的對比度隨著光程差Δ的增大而下降的定性結論，用積分法可以得出定量關係如下：
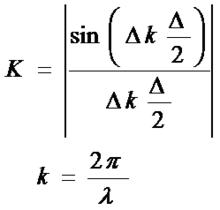干涉條紋對比度時間相干性
光波通過相干長度所需的時間稱為相干時間Δt。
由相干長度的定義可推知，同一光源在相干時間Δt內不同時刻發出的光波可以產生干涉，這種相干性稱為時間相干性，相干時間就是時間相干性的量度標誌。
干涉條紋對比度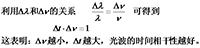
干涉條紋對比度