簡介
希爾伯特第16問題是著名數學家希爾伯特(Hilbert,D.)提出的涉及平面多項式系統極限環存在和分布問題的重要數學難題。
發展
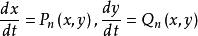希爾伯特第16問題1900年，希爾伯特在國際數學家大會上提出了23個數學問題，其中第16問題的後半部分是涉及微分方程的，他提出：右端為x,y的n次多項式P(x,y)，Q(x,y)的平面系統最多有幾個極限環，它們的位置分布如何?許多數學家圍繞這一問題開展研究，從而深入地推動了平面定性論及一些相關學科分支的研究。
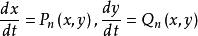希爾伯特第16問題迪拉克(Dulac,H.)於1923年發表長達140頁的論文，證明每一確定的系統其極限環只有有限個，稱之為有限性定理。
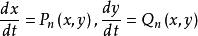希爾伯特第16問題但後人發現其證明存在缺陷，直至20世紀80年代末期有限性定理才被嚴格地加以證明，這分別由蘇聯的依廖申科和法國的埃加勒(Ecalle,J.)、馬蒂內(Martinet, J.)等人獨立地完成。其核心部分是證明不可能有無限多個極限環聚集在一個分界線環鄰近。
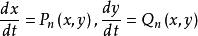希爾伯特第16問題解決希爾伯特第16問題，人們依不同的n來分別研究系統。n=1時，為線性系統，顯然不存在極限環。n=2時為二次系統。
20世紀50年代起，以葉彥謙和秦元勛為代表的中國數學家對其極限環的基本性質做了系統研究。
至20世紀末在國際上圍繞其極限環與全局結構等已有大量成果。鮑金(Bautin,N.N.)證明了二次系統在一個奇點外圍鄰近最多有三個極限環（1952年）。
20世紀70年代末，史松齡以及陳蘭蓀、王明淑等給出了具有不少於四個極限環的二次系統（其一個奇點外至少有三個，另一奇點外至少有一個）。
現狀
至今尚未能證明二次系統最多只能有四個極限環。
對於三次系統（即n=3時）也有不少研究成果，已經獲得了如下的實例：在一個奇點外圍鄰近聚集有8個極限環，也存在三次系統其相互嵌套著的極限環至少有11個。
對n≥4的系統則研究甚少。
總之，要徹底解決希爾伯特第16問題還有相當大的難度。
