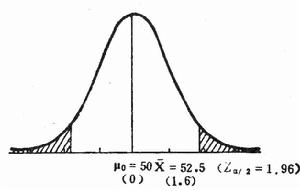
在統計學中,差異顯著性檢驗是“統計假設檢驗”(Statistical hypothesis testing)的一種,用於檢測科學實驗中實驗組與對照組之間是否有差異以及差異是否顯著的辦法。
在實驗進行過程中,儘管儘量排除隨機誤差的影響,以突出實驗的處理效果,但由於個體間無法避免的差異,以及諸多無法控制的因素,使得實驗結果最後表現的觀察值處理處理效應之外,還包括實驗誤差的效應。
因此對兩個樣本進行比較時,必須判斷樣本間差異主要是隨機誤差造成的,還是本質不同或處理效應引起的。
類型
t檢驗
適用於計量資料、常態分配、方差具有齊性的兩組間小樣本比較,檢驗兩個處理平均數的差異是否顯著。
spss提供的T檢驗有3種形式,分別是單樣本T檢驗(One-Sample T Test),獨立樣本T檢驗(Independent-Sample T Teat)和成對樣本T檢驗(Paired-Sample T Test)。
t'檢驗
套用條件與t檢驗大致相同,但t′檢驗用於兩組間方差不齊時,t′檢驗的計算公式實際上是方差不齊時t檢驗的校正公式。
U檢驗
套用條件與t檢驗基本一致,只是當大樣本時用U檢驗,而小樣本時則用t檢驗,t檢驗可以代替U檢驗。
方差分析
用於常態分配、方差齊性的多組比較,即多個處理平均數之間差異的顯著性檢驗。常見的有單因素分組的多樣本均數比較及雙因素分組的多個樣本均數的比較,方差分析首先是比較各組間總的差異,如總差異有顯著性,再進行組間的兩兩比較,組間比較用q檢驗或LST檢驗等。
卡方檢驗
是計數資料主要的顯著性檢驗方法。用於兩個或多個百分比(率)的比較。常見以下幾種情況:四格表資料、配對資料、多於2行乘以2列資料及組內分組卡方檢驗。
非參數檢驗
以上的參數檢驗都基於共同的兩個假設:正態性假定和方差齊性假定。但是,我們在實際工作中,不可能總是遇到滿足這兩個假定的統計數據,這時候,如果強行採用參數檢驗就會造成錯誤。此時,可以採用基於秩和的非參數檢驗,如Kruskal-Wallis檢驗,Friedman檢驗。