基本介紹
設在平面上點的齊次仿射坐標或射影坐標為(x,x,x),則滿足三元二次齊次方程
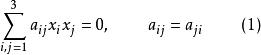 二階曲線
二階曲線的點的全體稱為 二階曲線。這裡a為實數且至少有一個不是零,該方程稱為這二階曲線的方程,(a)稱為係數矩陣,若係數矩陣的行列式|a|≠0,則二階曲線稱為非退化的,否則稱其為退化的,退化的二階曲線是兩條直線(可以是虛直線),在射影平面上,成射影對應的兩個線束的對應直線的交點的集合是二階曲線(參見本卷《平面解析幾何》中的“二次曲線”) 。
二階曲線的射影定義
定理1 兩個不共心的射影線束,其對應直線的交點集及該兩個線束的中心組成一條二階曲線。
定理1為二階曲線提供了幾何模型,是二階曲線的存在定理。形成二階曲線的兩個射影線束的中心,由定理知,似乎與曲線上的其它點並不“平等”。但由下述定理可知,其實不然。
定理2 一條由兩個射影線束的對應直線的交點構成的二階曲線上,任意兩點都可取作構成該曲線的兩個射影線束的中心。
定理3 平面上任意無三點共線的五點可決定一條由兩射影線束所成的二階曲線。
定理4 任何二階曲線都可由兩個射影線束所成。
定義1 兩射影線束對應直線的交點集稱為二階曲線。
特殊地,當射影對應是透視對應時,有:
兩透視線束對應直線的交點如前討論在透視軸上;且(圖1)在兩線束的公共直線SS'=t上的每一點,均是兩透視線束S和S'中對應直線SS'∈S和S'S∈S‘的交點。因此,二階曲線特殊地由兩條直線組成:一是透視軸,一是兩線束的公共線。
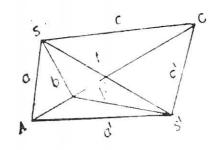 圖1
圖1定義2兩個不共心、非透視的射影線束所成的二階曲線稱為常態二階曲線。兩個透視線束所成的二階曲線稱為變態的二階曲線。
由於二階曲線和二級曲線從代數形式上看是一致的,都是二次方程,因此統稱為二次曲線 。
二階曲線上的射影變換
 二階曲線
二階曲線 二階曲線
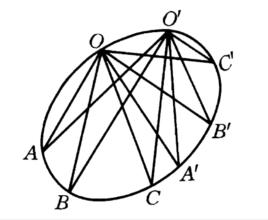
二階曲線二階曲線上的射影變換(projective transformation on curves of order 2)是一種特殊的射影變換,若在二階曲線的點之間建立了一一對應,使得二階曲線上任意一點與各組對應點相連所構成的兩個線束是射影對應的,則稱在二階曲線上建立了射影變換,二階曲線稱為底。如圖,若O(A,B,C,…)O(A′,B′,C′,…),則A→A′,B→B′,C→C′,…決定射影變換,記為(A,B,C,…)(A′,B′,C′,…),也稱它們為二階曲線上的射影點列,射影變換與O點的取法無關,二階曲線上的射影變換由三組對應點惟一決定,若給了二階曲線上的一個射影變換,則對於任意兩組對應點M,M′與N,N′,直線MN′與M′N的交點總在一條確定的直線上,這條直線就是已知變換的透視軸 。
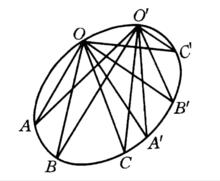 圖2
圖2二階曲線的極點
二階曲線的極點(pole of curve of order 2)射影幾何的基本概念之一.給定一個非退化的二階曲線Γ和不在Γ上的點P,過P作直線交Γ於M,M,若Q是直線PM上一點,且(MM,PQ)=-1,則稱P與Q關於二階曲線Γ調和共軛或關於Γ互為共軛點,點P關於二階曲線Γ的調和共軛點的軌跡是一條直線,稱為點P的 極線,點P稱為這直線的 極點。若點P在二階曲線上,則規定其極線就是它的切線。反之,切線的極點就是它的切點。這樣,對於非退化的二階曲線,極點和它的極線之間就建立了一一對應的關係。如果二階曲線為
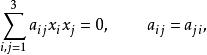 二階曲線
二階曲線則點p(p,p,p)的極線方程是
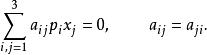 二階曲線
二階曲線反之,直線l[u,u,u]的極點P(p,p,p)的坐標可由下列方程組解出
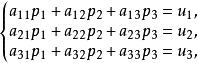 二階曲線
二階曲線二階曲線的奇異點
二階曲線的奇異點(singular point of curve of order 2)是二階曲線上的特殊點,簡稱奇點。即二階曲線(1)上滿足條件
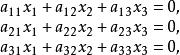 二階曲線
二階曲線的點P(p,p,p),二階曲線非退化的充分必要條件是無奇異點,退化二階曲線必有奇異點(可以是虛點),且當係數矩陣(a)的秩等於2時,有惟一奇異點;當(a)的秩等於1時,有無窮多個奇異點,它們在同一條直線上。二階曲線的奇異點有簡單的幾何意義:二階曲線上一點是奇異點的充分必要條件是它與曲線上任何點的連線含於此曲線上 。
二階曲線上的對合
二階曲線上的對合(involution on a curve of order 2)是指二階曲線上的一種特殊射影變換,若在二階曲線上的點之間建立了非恆等的一一對應,以曲線上任一點為中心與曲線上對應點的連線構成兩個線束,如果這兩個線束是對合的,則稱在二階曲線上所建立的對應是對合,二階曲線上的對合由兩對對應點惟一確定 。
二階曲線的射影分類
二階曲線的射影分類(projective classification of curve of order 2)是二階曲線的一種分類方法,指用射影等價關係對二階曲線進行的分類。射影平面上的二階曲線(1)的集合在射影群之下分為五個射影類,其標準方程和曲線名稱分別為:
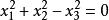 二階曲線
二階曲線1., 非退化的實二階曲線。
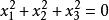 二階曲線
二階曲線2., 非退化的虛二階曲線。
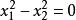 二階曲線
二階曲線3.,一對實直線。
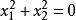 二階曲線
二階曲線4.,一對虛直線。
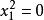 二階曲線
二階曲線5.,一對重合直線。
在同一類里的任意兩條二階曲線射影等價,即存在某一射影變換,將其中一條曲線變為另一條曲線。而不同類中的任意兩條曲線不射影等價 。
二階曲線的內接n點形
二階曲線的內接n點形(inscribed n-gon of curve of order 2)是指頂點都在一個非退化二階曲線上的n點形,若一個n點形(簡單的或完全的)的頂點都在一個非退化二階曲線上,則這個n點形稱為該二階曲線的內接n點形(簡單的或完全的) 。