完全隨機化設計的含義
完全隨機化設計
完全隨機化設計 完全隨機化設計完全隨機化設計是指用隨機化的方法處理指派試驗序號和試驗對象的試驗設計。在此種試驗設計中僅有一個試驗因素，分為個水平，用隨機化的方法將試驗單元分為組，每個試驗組被隨機地指派接受一種試驗處理 。
當我們採用完全隨機化設計時，應將各種處理隨機地指派給各個實驗單元。比如說，假定我們想對4 種商標的輪胎A、B、C 和D作行駛試驗，以確定這幾種輪胎的期望里程數之間有無差別。這時，我們可以對每一種商標取10個輪胎並隨機地把它們安裝在20輛汽車的後輪上，然後駕駛這些汽車，直到輪胎達到預定磨損量為止，同時記下所行駛的里程數。根據方差分析，我們可以對這些輪胎的期望里程數是否相等作出決策。在這裡，被我們隔離的兩個變差來源為由於處理(商標) 不同而產生的變差以及殘差，後者即除輪胎外所有其他原因所造成的變差。
對於採用完全隨機化設計的實驗，其數據的分析方法就是所謂 單向方差 分析。取這樣的名稱是由於我們僅僅根據一個準則，即實驗單元所屬的一組處理來對實驗單元(從而對所得到的計量值) 進行分類之故。
完全隨機化設計也可以用單向方差分析來分析從抽樣調查中得到的數據。這裡所說的抽樣調查，是指從若干個總體各取一個隨機樣本。這種能使研究者檢驗若干個平均值之間有無顯著差別的單向方差分析法，實際上不過是檢驗兩個平均值之間有無差別的-檢驗法的推廣而已 。
試驗設計
試驗設計(design of experiment，DOE )是以機率論和數理統計為理論基礎，經濟、科學地安排試驗以收集樣本數據的一項技術。其中，收集樣本數據的過程稱為 試驗。
試驗設計是通過 明確試驗指標、 尋找影響試驗指標的可能因素、根據實際問題 選擇適 用的 試驗設計方法和 方差分析法科學分析試驗結果等四個步驟科學安排試驗，使人們用儘可能少的試驗獲得儘可能多的可靠結論。試驗設計必須遵循的 三個基本原則，即重複(replication)、隨機排列(randomization)和局部控制(local control)。 重複是指試驗中將同一試驗處理設定在兩個或兩個以上的試驗單元( 接受各試驗水平的對象稱為試驗單元( experiment unit )) 上；同一試驗處理所設定的試驗單元數稱為重複數，可重複性就是在每個試驗條件下試驗是可重複進行的。 隨機排列是指試驗的每一個處理都有同等機會設定在一個重複中的任何一個試驗小區上。 局部控制指當試驗單元之間差異較大時，即存在某種系統干擾因素時，可以將全部試驗單位按干擾因素的不同水平分成若干個小組，在小組內部使非試驗處理因素儘可能一致，實現試驗條件的局部一致性。
試驗設計包括 完全隨機化設計、 隨機化區間設計、 因子設 計、 正交設計等不同類型的設計方法。
完全隨機化的設計過程
下面通過一個具體的例子來說明 完全隨機化的設計過程。
試驗設計包括明確試驗指標、尋找影響試驗指標的可能因素、根據實際問題選擇適用的試驗設計方法、科學分析試驗結果等四個步驟。
例如，某一食品公司研發了一種新的食品，先需要考察其市場銷售量的影響因素。其中，食品的銷售量就是試驗的指標，經過經驗分析和同行比較，發現可能影響試驗指標的是食品包裝的因素，其有三種不同的包裝:包裝1、包裝2 和包裝3。為適應市場的需要，須研究確定不同的食品包裝對其銷售量是否有影響。為此需要選擇一些超市( 假設所選超市地理位置、經營規模都相仿，可視為試驗環境相同)，在每個超市銷售不同包裝的產品，然後收集其實際銷售量，進而分析食品的包裝對銷售量的影響是否顯著。這一過程就是試驗設計的過程，下邊我們給出完全隨機化設計的基本步驟，由於單因素完全隨機化設計只涉及一個因素，顯然滿足 “局部控制” 原則（參見上文實驗設計的三個基本原則）。
“隨機化”的設計過程
這裡的“食品包裝”是試驗因素，“包裝1、包裝2 和包裝3”是因素的三個水平，選取三個超市為試驗單元，然後將每個包裝的產品隨機指派給其中的一個試驗單元，如包裝1可以隨機指派給超市2，包裝2可以隨機指派給超市3，剩餘的包裝3指派給超市1。
“可重複性”的設計過程
完全隨機化設計除符合“隨機化”要求外，還必須符合“可重複性”原則。上例中由於只抽取了3 家超市作為試驗單元，只能獲得3 個銷售量的數據，也就是對於每個處理的樣本容量為1。為了獲得每個包裝更多銷售量的數據，必須重複基本試驗步驟。例如，假定而是15家超市，然後將每個包裝隨機指派給其中的5 家超市，這不是抽取了3 家超市，就相當於重複做了5 次試驗 。
在滿足設計規則和要求之後就可以獲取試驗數據
三種不同包裝的食品在15 家超市的銷售量樣本數據如表1所示。
| 銷售量 | |||||
| 包裝1 | 37 | 35 | 33 | 34 | 38 |
| 包裝2 | 33 | 30 | 32 | 35 | 35 |
| 包裝3 | 46 | 43 | 40 | 43 | 45 |
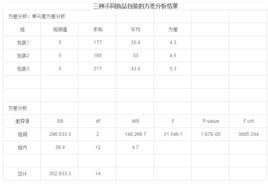
有了試驗數據後，需要分析每個包裝的銷售量均值是否相同，也就是要分析不同包裝對銷售量的影響是否顯著。顯然， 分析完全隨機化設計的方法就是 單因素方差分析法。通過計算，由表1的數據得到的分析結果如表2所示。
| 方差分析：單元素方差分析 | ||||||
| 組 | 觀測值 | 求和 | 平均 | 方差 | ||
| 包裝1 | 5 | 177 | 35.4 | 4.3 | ||
| 包裝2 | 5 | 165 | 33 | 4.5 | ||
| 包裝3 | 5 | 217 | 43.4 | 5.3 | ||
| 方差分析 | ||||||
| 差異源 | SS | df | MS | F | P-value | F crit |
| 組間 | 296.533 3 | 2 | 148.266 7 | 31.546 1 | 1.67E-05 | 3885 294 |
| 組內 | 56.4 | 12 | 4.7 | |||
| 總計 | 352.933 3 | 14 | ||||
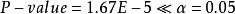完全隨機化設計
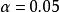完全隨機化設計從方差分析數據可看出，由於(這裡取顯著性水平)，表明食品的包裝對銷售量有顯著的影響 。
